physics user1
Homework Statement
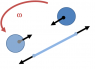
[/B]there's an image of the situationHomework Equations
[/B]F= mω^2 RThe Attempt at a Solution
[/B]so, in the image there are two spheres that exerts a tension on the string using their centrifugal, since the centrifugal bodies are two I expect that the tension is the sum in intensity of the two forces, do you agree? Another question is: why the centrifugal forces acts to the string? Aren't these forces supposed to act just on the spheres?Attachments
Last edited by a moderator: