joe465
- 93
- 0
Homework Statement
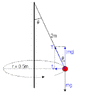
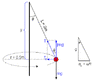
Calculate the tension in a 2m string attached to a 2kg bob that is moving in
horizontal circles of 0.5m radius.
Homework Equations
I thought it was F=MA but the working out shows all sorts
The Attempt at a Solution
I know the answer is 78.4N but don't know how to get there.