You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
AI Thread Summary
The discussion revolves around understanding the relationship between tensions T1 and T2 in a pulley system with two masses, 2m and m. It is clarified that if the pulley is massless and frictionless, the tensions on both sides of the pulley will be equal, meaning T1 equals T2. However, if the pulley has mass, the tensions can differ, and the moment of inertia must be considered. The confusion arises from the assumption about which tension corresponds to which mass, but ultimately, the consensus is that T1 and T2 are equal when the system is balanced. The key takeaway is that in a massless and frictionless scenario, T1 does not exceed T2.
Physics news on Phys.org
shanykool
- 2
- 0
T=2m1m2g
----------
(m1+m2)
----------
(m1+m2)
shanykool
- 2
- 0
t2 would be greater if the mass in t2 is greater than the mass in t1
Doc Al
Mentor
- 45,578
- 2,435
Is the pulley massless and frictionless? That's the key.physics kiddy said:I have attached a pic with my question. I want to know if T1>T2 or not.
Careful! That's not true. In general you'll have to solve for the tension in the string by applying Newton's 2nd law.As much as I know, Tension in a string = Earth's Gravitational force.
physics kiddy
- 135
- 1
T1 has a mass greater than T2.
Doc Al
Mentor
- 45,578
- 2,435
I don't know what you mean. T1 and T2 are tensions. Regardless of the size of the mass on the ends of the string segment, the tension on both sides of a massless and frictionless pulley will be the same.physics kiddy said:T1 has a mass greater than T2.
Since the mass on each side of the pulley is the same (2m on each side, added up), it turns out that in this particular case the tension T1 = T2 = 2mg. (The masses don't accelerate.)
technician
- 1,506
- 18
Agree completely with DocAl and will add that the tension in a string is the same everywher... all the way along it.
There is no resultant force on this system so it is either at rest or moving with constant velocity (speed) in one direction or the other.
The only string with a different tension is between the 2 masses m and m ...the tension in here will be mg
The tensions T1 and T2 will be 2mg
There is no resultant force on this system so it is either at rest or moving with constant velocity (speed) in one direction or the other.
The only string with a different tension is between the 2 masses m and m ...the tension in here will be mg
The tensions T1 and T2 will be 2mg
briantaekim
- 7
- 0
I personally think that T2 was meant for the second string connecting the masses on the right side of the pulley. Because usually the pulley doesn't have mass (for beginner class) and the tension is uniform in one continuous string (and this is assumed rather than stated). So... I worked out the problem w these assumptions below. Check it out. So the solution looks like T1>T2.
Attachments
cupid.callin
- 1,130
- 1
technician said:Agree completely with DocAl and will add that the tension in a string is the same everywher... all the way along it.
Only if the string is also of negligible mass
And if the pulley has some mass, you can find its moment of inertia and apply the equations of torque:
T_1 R - T_2 R = I\alpha = \frac{Ia}{R}
Here I is moment of inertia of pulley and R is its radius ...
And if pulley has no mass, I=0 ...
physics kiddy
- 135
- 1
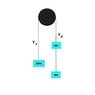
I apologize for confusing you all. I am sorry. I have cleared my doubts with the question. The question was that there's a pulley and two masses 2m and m are tied to the opposite ends of the pulley as shown in the figure. The tension between 2m and pulley is T1 and between m and pulley is T2. Is the tension T1>T2?
The pulley and string are assumed to be massless and frictionless.
The pulley and string are assumed to be massless and frictionless.
Attachments
Last edited:
Doc Al
Mentor
- 45,578
- 2,435
Are you sure that T2 refers to the tension between m and the pulley and not between m and m?physics kiddy said:The tension between 2m and pulley is T1 and between m and pulley is T2.
(Is this your diagram, or the one given with the problem?)
physics kiddy
- 135
- 1
Yes, I am sure.
Doc Al
Mentor
- 45,578
- 2,435
In that case, your question has already been answered.physics kiddy said:Yes, I am sure.
physics kiddy
- 135
- 1
I can't figure out where the answer is. Please explain it once again. Thanks
Doc Al
Mentor
- 45,578
- 2,435
See post #6.physics kiddy said:I can't figure out where the answer is. Please explain it once again. Thanks
Similar threads
- Replies
- 22
- Views
- 962
- Replies
- 7
- Views
- 1K
- Replies
- 47
- Views
- 3K
- Replies
- 2
- Views
- 2K
- Replies
- 10
- Views
- 2K
- Replies
- 34
- Views
- 3K
- Replies
- 5
- Views
- 3K
- Replies
- 2
- Views
- 794
- Replies
- 1
- Views
- 2K
- Replies
- 5
- Views
- 3K
Hot Threads
-
Torque biomechanics
- Started by Naucus
- Replies: 6
- Introductory Physics Homework Help
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
-
How do you calculate the pull of this piston?
- Started by vdance
- Replies: 27
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 7
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math