Tension in Rope Wrapped Around a Rod

[Poetria]

Homework Statement

I solved the first part of the problem correctly. Here there is the second part:
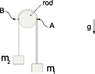
assume that m1 is large enough so that the rope starts to slip and the masses start to move. What is a, the magnitude of the acceleration of the masses after sliding has begun?

Hint: Just when the masses start moving, the relationship between T_A

and T_B becomes T_B=T_A*e^(-mu_k*pi), where mu static is replaced by mu kinetic.

m_1>m_2
theta = pi

Homework Equations

I guess I have include the friction force and use the Capstan equation to do so but I am lost.

The Attempt at a Solution

T_1>T_2
T_1 = T_A (from the first part)
T_1 = T_2 + F_f (friction on the contact surface)

m_1*g-T_A=m_1*a_1
T_B-m_2*g = m_2*a_2

I tried to experiment with the moment of inertia but it wasn't covered in the course. Any hint what to do next? I am still left with T_A, when I try to calculate acceleration.

 

[haruspex]

I am still left with T_A, when I try to calculate acceleration.

I don't see how. You know the relationship between T_A and T_B, and the relationship between a₁ and a₂. Four equations, four unknowns.

 

[Poetria]

I see.
Is this correct:

for T_A:

m_1*g-T_A=T_A*e^(-mu_k*pi)-m_2*g

since m_1*a_1=m_2*a_2

finally I got:
T_A=(g*m_1+m_2)/(1+e^(-mu_k*pi))a*(m_1+m_2)= m_1*a_1-m_2*a_2

The right side:
T_A-m_1*g-T_B+m_2*g = T_A*(1-e^(-mu_k*pi))+g*(m_2-m_1)

So
a = ((g*(m_1+m_2)/(1+e^(-mu_k*pi)))*(1-e^(-mu_k*pi))+g*(m_2-m_1))/(m_1+m_2)

It looks complicated.

 

[haruspex]

since m_1*a_1=m_2*a_2

Um, why?

 

[Poetria]

Um, why?

I thought this is because mass 1 and mass 2 are connected.

 

[haruspex]

I thought this is because mass 1 and mass 2 are connected.

Yes, but by what, exactly?

 

[Poetria]

Yes, but by what, exactly?

By a rope of course. I thought net force for 1 should be equal in magnitude to net force for 2. I guess I don't understand it. :(

 

[haruspex]

By a rope of course.

Right, not a length of elastic.

 

[Poetria]

Right, not a length of elastic.

Yes, It won't stretch. It is just like taking derivatives of the length of a rope. Acceleration is its second derivative.
So is just a_1=a_2?

 

[haruspex]

Yes, It won't stretch. It is just like taking derivatives of the length of a rope. Acceleration is its second derivative.
So is just a_1=a_2?

Right.

 

[Poetria]

Right.

Thanks. I got the right answer. Phew.

 

[swaqqiali]

Right.

It should be (a_1 = - a_2). Correct me if i am wrong.

 

[haruspex]

It should be (a_1 = - a_2). Correct me if i am wrong.

If you look at the equations in post #1 you will see that a₁ is being defined as positive down while a₂ is defined as positive up. a₁=a₂.

 

[swaqqiali]

If you look at the equations in post #1 you will see that a₁ is being defined as positive down while a₂ is defined as positive up. a₁=a₂.

yes, i missed that, thank you.