Tension in two cables with a mass

[d.tran103]

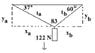
Hey guys, I'm having trouble analyzing the picture created in this and answering it. I believe it forms a triangle with angles 37, 60, and 83? Are the x components for both sides the same? Are the y components of both sides the same? If anybody has step by step details on how this solve this that would be greatly appreciated. Thanks!

A traffic light weighing 122 N is supported by two cables, the first at an angle of 37 degrees below the horizontal from the horizontal support beam to which it is affixed, to the left and above the traffic light. To the right, a second cable is at an angle of 60. degrees below the horizontal. What is the tension in the 60. degree cable?
a) 82.7
b) 111
c) 134
d) 98.1

 

[tiny-tim]

welcome to pf!

hi d.tran103! welcome to pf!

if you're trying to draw the actual triangle, it doesn't matter …

the tension will be the same no matter how long the cables are

but if you're trying to draw the vector triangle then the three sides correspond to the two tension forces (parallel to the two cables) and the weight (vertically down), and the forces are proportional to the lengths of the sides

 

[d.tran103]

hi d.tran103! welcome to pf!

if you're trying to draw the actual triangle, it doesn't matter …

the tension will be the same no matter how long the cables are

but if you're trying to draw the vector triangle then the three sides correspond to the two tension forces (parallel to the two cables) and the weight (vertically down), and the forces are proportional to the lengths of the sides

Hey thanks but I am still really confused. You have to guide me in baby steps lol. So I drew a picture of my thing. I think that you and yb are both 61 but I am not sure. That is throwing me off. Can you help me from there? Thanks!

 

[d.tran103]

hi d.tran103! welcome to pf!

if you're trying to draw the actual triangle, it doesn't matter …

the tension will be the same no matter how long the cables are

but if you're trying to draw the vector triangle then the three sides correspond to the two tension forces (parallel to the two cables) and the weight (vertically down), and the forces are proportional to the lengths of the sides

does ta = tb?

 

[d.tran103]

is set it up as ta = tb = x. xsin60 +xsin37 = 122. Then I got 83.1. That's the closest answer I've had so far but it doesn't seem right to me?

 

[tiny-tim]

are you trying to draw the vector triangle ?

if so, read again what i said …

one of the side has to be vertical! ​

 

[d.tran103]

are you trying to draw the vector triangle ?

if so, read again what i said …

one of the side has to be vertical! ​

hey what do you mean one side has to be vertical? I'm completely lost

 

[tiny-tim]

a vector triangle (or force triangle) has one side for each force

each side is parallel to the force, and proportional to its magnitude

the force for the weight is vertical, so that side of the trianhle has to be vertical

 

[d.tran103]

Oh okay. So I should set it up as xsin60 +xsin37 = 122 (with x being the tension)? And the tensions are equal and don't depend on length?

 

[tiny-tim]

no, the tensions are only equal if the sides are equal

you have a triangle, and you know one length and two angles …

use the cosine and/or sine rules to find the other lengths

(if you don't know the cosine and sine rules, look them up)

 

[tiny-tim]

Hi Peter G.!

Hi, I am studying for a test on Static Equilibrium and I was going through some topics on the Forums. I came across "The Tension in two cables with a mass" and found it quite challenging compared to the problems I dealt with before, so, being a person who does not like being defeated I went for it:

So, the Traffic Light is in static equilibrium. If we draw the Weight Force and the Two tensions in a Vector Diagram we get a closed triangle. In doing so, I had one side, the weight, 122 N and worked out the angles: 30, 53 and 97. I used the sine rule and got:
122 x sin 53 / sin 97 and got 98.2, not 98.1 as he listed as one of the multiple choice answers.

I was wondering: Was it a coincidence that I got a very close answer despite doing the wrong work out or am I right?

No, I think you're right

 

[Peter G.]

Thanks