Tension in two ropes with a mass hanging from them

[flemonster]

Homework Statement

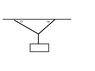
The two angled ropes used to support the crate in the figure below can withstand a maximum tension of 1900 N before they break.


A.) Which of the ropes would break first?

B.) What is the largest mass the ropes can support before breaking?

Homework Equations

F = ma
Weight force = mg

The Attempt at a Solution

A.) I got the answer to this by taking 1900 for the tension in each rope and figuring out the y-components of the tension with the equation:

Ty = 1900 * sinθ

This gave me 950 for the 30° rope and 1344 for the 45° rope. That means the 45° rope will break first.

B.) I'm not sure if I'm on the right track here but I'll show what I came up with. Since I know the 45° rope will break first then I can pretty much ignore the other rope and figure out the mass that will make the 45° rope snap. I said:

1900*sin45 = 9.8m

That gave me a mass of 137 kg. Whaddaya think? Is it on?

*I realize the angles in the pic are not to scale. Please forgive the hastily drawn paintbrush pic.

 

[haruspex]

A.) I got the answer to this by taking 1900 for the tension in each rope and figuring out the y-components of the tension with the equation:

Ty = 1900 * sinθ

This gave me 950 for the 30° rope and 1344 for the 45° rope. That means the 45° rope will break first.

I don't see how that follows. If each is at 1900N total why should either snap first?
The truth, of course, is that they would not be at the same tension. You need to get equations for what their tensions would be.

B.) I'm not sure if I'm on the right track here but I'll show what I came up with. Since I know the 45° rope will break first then I can pretty much ignore the other rope and figure out the mass that will make the 45° rope snap. I said:

1900*sin45 = 9.8m

No.
How many forces are acting on the mass? What is the component of each in the vertical direction?

 

[flemonster]

I don't see how that follows. If each is at 1900N total why should either snap first?
The truth, of course, is that they would not be at the same tension. You need to get equations for what their tensions would be.

No.
How many forces are acting on the mass? What is the component of each in the vertical direction?

So I'm basing my assumption that the first part is right on a practice midterm we did in class. My first thought when looking at the problem was that the 1900 N would be distributed through the two ropes, but my instructor set up the problem as if each rope could withstand up to 1900 N, not that the combined tolerance of the ropes was 1900 N. Is that what seems wrong in my calculations or is it something else?

Should I be thinking about the sum of the y-forces as:

[T30*sin(30)] + [T45*sin(45)] - w = 0

where T30 = tension in the 30° rope and T45 = tension in the 45° rope? But if that's the case then how would I go about finding which would break first? I know that T30 + T45 = 1900, but would that come into play?

It's the second part of the problem that I got wrong. Thinking about the forces acting on the mass would give me a weight force and two tension forces, right? Since the weight force is going down then subtracting the sum of the y-components of the tension forces should equal zero so long as the mass in in equilibrium. But since my calculations in this part are based on the assumption that the 45° rope will break first I'm not sure how to proceed.

 

[haruspex]

my instructor set up the problem as if each rope could withstand up to 1900 N, not that the combined tolerance of the ropes was 1900 N.

I've no argument with that. My point is that supposing each is experiencing 1900N is not a valid way to proceed. They simply won't be.

Should I be thinking about the sum of the y-forces as:

[T30*sin(30)] + [T45*sin(45)] - w = 0

Yes.

then how would I go about finding which would break first?

You need a second equation. x-forces?

It's the second part of the problem that I got wrong.

You may have got the right answer to the first part, but only by luck. When you correct that, the rest of the problem should be easy.

 

[flemonster]

You need a second equation. x-forces?

I think the sum of the x-forces would be T30*cos(30) + T45*cos(45) = 0. But how does that come into play? If mass is added to the crate then wouldn't it be just the y-components that matter? Is that assuming too much?

 

[haruspex]

I think the sum of the x-forces would be T30*cos(30) + T45*cos(45) = 0.

Careful with your signs.

If mass is added to the crate then wouldn't it be just the y-components that matter?

No. The (correct version of the) equation above will tell you how the load is shared between the two cables. That is what determines which will break. Only when you have figured out the sharing do you know what the y components will be.