Tension of cables of unequal length

AI Thread Summary
In the discussion about the tension in cables of unequal lengths supporting a uniform mass, the main question revolves around whether the tensions T1 and T2 are equal. It is suggested that if the tensions were unequal, the mass would rotate around its center of mass, indicating that the tensions must indeed be equal to maintain equilibrium. The calculation of tension involves analyzing the forces and moments acting on the mass. The conversation emphasizes the importance of considering the center of mass and the balance of forces. Ultimately, for a uniform mass suspended by unequal cables, the tensions must be equal to prevent rotation.
mikejones222
Messages
2
Reaction score
0
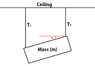
While doing some "what is the tension in cable" of hanging masses problems, I thought of the following scenario: a mass, uniform in density, is suspended by two cables of unequal length (See attachment)

Assuming that the mass is uniform in density, would T1 be the same as T2? Intuitively, it seems as though T1 may be less, but wasn't sure. If it's not, then how would one go about calculating the tension?
 

Attachments

  • mass hanging slanted.png
    mass hanging slanted.png
    7 KB · Views: 577
Physics news on Phys.org
Hi mikejones222! http://img96.imageshack.us/img96/5725/red5e5etimes5e5e45e5e25.gif

You draw the 3 forces: what you've shown together with weight acting down through the centre of mass. Sum of moments about any convenient point = 0. :wink:
 
Last edited by a moderator:
riiiight...if tensions were unequal, then the mass would rotate around it's center of mass...thanks:)
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Problem involving space elevators
Replies
19
Views
2K
Why are the forces on torque tension and not the weight of the mass?
Replies
7
Views
1K
Tension and net torque in a cable
Replies
10
Views
5K
Tension in a deformed cylindrical bag on a surface
Replies
18
Views
1K
How do I calculate the tension in cable 1 without using the tension in cable 2?
Replies
2
Views
5K
Why is the tension in a massive cable always tangent to its portion?
Replies
5
Views
2K
Equilibrium : normal reaction of a rotational center?
Replies
2
Views
1K
What Are the Tensions in Each Cable of a Suspension Bridge?
Replies
31
Views
4K
"Tension: T1 vs T2 - What is Correct?
Replies
1
Views
2K
Force to move a catenary curve
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top