iJamJL
- 58
- 0
Homework Statement
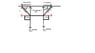
The ends of a massless rope are tied to a ceiling. Two identical 4.21 kg masses are now hung along the length of the rope, dividing the rope into three segments of equal length. Segment 2 (the central segment) is horizontal (parallel to the ceiling). The ends of segments 1 and 3 are attached to the ceiling, making an angle of 50.2° with the ceiling. (The distance between the points at which the rope is hung is greater than the rope segments.) Find the magnitude of the tension in rope 2.
Homework Equations
Pythagorean and components
The Attempt at a Solution
I attached my diagram of how I drew everything. I'm hoping that this is correct. If it is, then I assume rope 2 is the middle section of the rope where it is parallel with the ceiling (my professor doesn't seem to phrase his questions that well, or I'm just not used to it). After solving for the tensions in rope 1 and 3, which are equal to each other, we could move the x-component vector to where I made it in red. These two vectors act in opposite directions, causing the tension of the middle rope to be twice as much. That is my assumption.
If my assumption is correct, then the tension in rope 2 should be:
T*cos(50.2)*2=68.82
This answer is incorrect, so could someone tell me where I went wrong?
 …
…