What happens to the angle between two wires when one current is doubled?

AI Thread Summary
When the current in one of the wires is doubled, the magnetic force acting on that wire increases, leading to a change in the angle between the two wires. The tension in the wires and the gravitational force must also be considered, as they affect the equilibrium of the system. The relationship T1sinθ1 = T2sinθ2 is crucial for analyzing the angles, and the forces involved will not remain equal due to the increased current. Newton's third law implies that the forces will adjust, resulting in a new angle for the wire with the doubled current. Ultimately, the angle will be larger than it was before the current was increased.
Eitan Levy
Messages
259
Reaction score
11

Homework Statement


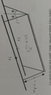
We have two very long wires, each with the same mass of 20 grams per meter. They are hung from the ceiling with two identical wires. When they both had the same current flowing to the opposite directions, they created the same angle.
We double the current in one of them, is the angle that they will create (as shown in the picture) will be the same again?

Homework Equations


F=BIL

The Attempt at a Solution


I couldn't prove it. I am stuck with T1sinθ1=T2sinθ2.
Is there any assumption I am supposed to make? I know that the forces are tension, gravity and magnetic force, and I understand what their directions are.
 
Physics news on Phys.org
The picture:
 

Attachments

  • ‏‏לכידה.PNG
    ‏‏לכידה.PNG
    9.8 KB · Views: 459
What does Newton's 3rd law say? What does that imply for the two angles? Will they be equal? Will they be the same or larger than before one of the currents was doubled?
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Electromagnetism question -- Forces between two current carrying wires
Replies
7
Views
3K
What is the net force on the current loop?
Replies
8
Views
2K
Magnetic Forces on infinite current-carrying wires
Replies
9
Views
2K
How Does a Magnetic Field Affect a Wire Carrying Current?
Replies
2
Views
1K
Why is magnetic field B along a straight wire circular not radial?
Replies
14
Views
3K
A confused Compass Needle between two solenoids
Replies
31
Views
2K
Moving charge deflected by a loop of wire
Replies
1
Views
709
Net force between two conducting strips
Replies
6
Views
844
Calculation of torque and force on magnetic dipole near infinite wire
Replies
3
Views
1K
When will two current-carrying wires touch each other
Replies
9
Views
2K

Hot Threads

Recent Insights

Back
Top