stunner5000pt
- 1,443
- 4
Test Stokes' Theorem for the function
\vec{v} = (xy) \hat{x} + (2yz) \hat{y} + (3yz) \hat{z} /
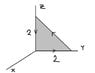
for the triangular shaded region
\int_{S} (\grad \times v) \dot da = \oint_{P} v \bullet dl
for the left hand side
\int_{0}^{2} \int_{0}^{2} (-2y \hat{x} - 3z \hat{y} - x \hat{z}) \hat{x} dy dz = \int_{0}^{2} \int_{0}^{2} (-2y) dy dz = \left[ \frac{-y^2} \right]_{0}^{2} \int_{0}^{2} dz = (-4)(2) = -8
so far so good??
ok for hte right hand side
i) x=0, z=0, v \bullet dl = 2y dy integration limits 0 to 2
ii) x=0, y=2, v \bullet dl = 0 dz integration from 0 to 2
i am not sute about the last one though...
am i right with i and ii though??
thank you for any advice!
\vec{v} = (xy) \hat{x} + (2yz) \hat{y} + (3yz) \hat{z} /
for the triangular shaded region
\int_{S} (\grad \times v) \dot da = \oint_{P} v \bullet dl
for the left hand side
\int_{0}^{2} \int_{0}^{2} (-2y \hat{x} - 3z \hat{y} - x \hat{z}) \hat{x} dy dz = \int_{0}^{2} \int_{0}^{2} (-2y) dy dz = \left[ \frac{-y^2} \right]_{0}^{2} \int_{0}^{2} dz = (-4)(2) = -8
so far so good??
ok for hte right hand side
i) x=0, z=0, v \bullet dl = 2y dy integration limits 0 to 2
ii) x=0, y=2, v \bullet dl = 0 dz integration from 0 to 2
i am not sute about the last one though...
am i right with i and ii though??
thank you for any advice!
Attachments
Last edited by a moderator: