Settho
- 4
- 0
- Homework Statement
- Show that the wave function is an eigenfunction of the hamiltonian.
- Relevant Equations
- Hamiltonian, wave function, energy and Born radius
Hello!
I am stuck at the following question:
Show that the wave function is an eigenfunction of the Hamiltonian if the two electrons do not interact, where the Hamiltonian is given as;
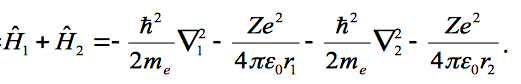
the wave function and given as;
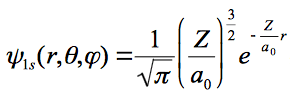
and the energy and Born radius are given as:
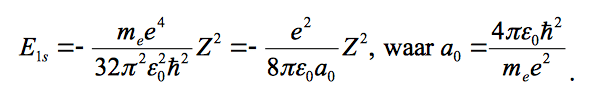
and I used this for ∇ squared:
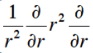
I am stuck at the end of the calculation. I know Z = 2, but somehow I don't end up with the energy, which you need to show that it is indeed an eigenfunction. This is what I get and where I am stuck at:
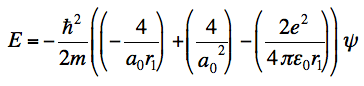
and even when I substitute a0 in this formula, I don't get the energy value. I honestly don't know where it did go wrong.
If someone is able to help, that would be great.
I am stuck at the following question:
Show that the wave function is an eigenfunction of the Hamiltonian if the two electrons do not interact, where the Hamiltonian is given as;
the wave function and given as;
and the energy and Born radius are given as:
and I used this for ∇ squared:
I am stuck at the end of the calculation. I know Z = 2, but somehow I don't end up with the energy, which you need to show that it is indeed an eigenfunction. This is what I get and where I am stuck at:
and even when I substitute a0 in this formula, I don't get the energy value. I honestly don't know where it did go wrong.
If someone is able to help, that would be great.