I Is the Killer Crate Paradox Resolved?

[PeterDonis]

The crate is to be launched at speed of ~0.70711c at an azimuth angle of 45° relative to the ground.

In other words, you are stipulating that Alice's description in the OP is correct?

 

[Gamma Anon]

But the OP has not stipulated that. He thinks there's some sort of paradox involved, because he thinks that his OP is describing a single scenario. But it isn't, and there isn't any paradox here at all. There is just a failure on his part to stipulate which of two distinct scenarios (the one that Bob's description in the OP is a valid description of, and the one that Alice's description in the OP is a valid description of) he wants to discuss.

Alice and Bob form their respective opinion based on different frames of reference (Alice uses the ground and Bob uses the train), they do not know which description is valid description.

All they know is that the Assassins intend to launch the crate (500mm x 500mm x 500mm) in the North East direction (Azimuth angle 45°) at a speed of 0.70711c (or exactly (0.5c)^0.5 ).

In each of their opinions they have made assumptions about the orientation of the crate relative to the window. Bob has assumed that due to the dimensions of the window matching that of the crate's faces, that the assassins intend to launch the crate face first at the window and not at angle (it won't go in otherwise).

Alice has assumed the crate prior to launch has each of its vertical faces orientated to exactly face North, South, East and West. Once launched however, orientation of these changes due to length contraction.

Are they distinct scenarios and thus Alice and Bob shouldn't be comparing them?

What would crate orientation need to be for Alice's perspective to match Bob's?

 

[Orodruin]

All they know is that the Assassins intend to launch the crate (500mm x 500mm x 500mm) in the North East direction (Azimuth angle 45°) at a speed of 0.70711c (or exactly (0.5c)^0.5 ).

As specified above, this is insufficient information. Even without special relativity, whether it goes in or not depends on orientation. The new thing with special relativity is Wigner rotation.

If they are distinct scenarios and thus Alice and Bob shouldn't be comparing them. How should the assassins orientate the the crate prior to launch so the plot will be successful?

In such a way that their setup matches Bob’s setup would be the obvious answer.

 

[PeterDonis]

Alice and Bob form their respective opinion based on different frames of reference

It's not a matter of opinions or frames of reference. The initial conditions for how the crate is launched need to be properly specified. Right now, as your OP stands, they are not. "Properly specified" means "a specification that can be translated into invariant terms, i.e., terms that do not depend on any choice of frame of reference". There is no such specification in your OP as it stands now.

All they know is that the Assassins intend to launch the crate (500mm x 500mm x 500mm) in the North East direction (Azimuth angle 45°) at a speed of 0.70711c (or exactly (0.5c)^0.5 ).

Angle 45 degrees relative to what? Speed of 0.70711c relative to what? Ideally these things would be specified relative to some actual object, not just a "frame", and the object's own state of motion would be specified as well.

Also, since the crate is not a point object (if it were this scenario would be a non-problem), it's not enough just to specify an initial velocity of one point. You need to specify enough to determine a unique state of motion for the crate as a whole. You haven't.

 

[PeterDonis]

In each of their opinions they have made assumptions about the orientation of the crate relative to the window.

And their assumptions are inconsistent with each other, so they do not describe the same scenario, they describe different scenarios. That is why they are coming up with different answers.

 

[Gamma Anon]

Please reread all of the replies you have obtained. The scenario you are describing here is not the same scenario that Bob is describing.

To abbreviate some of the replies (somewhat excessively), Bob and Alice are not describing the same scenario, so the outcomes are different, thus problem solved.

If the scenarios are different, then it has to do with differences in the crate's launch conditions, but what those differences are has not been well explained (At least not well enough for me to have a good understanding of why these are two different scenarios)

Let's consider a more well defined launch scenario:

The assassins intend to launch the crate in a two step process, with each of the faces starting at an initial orientation, while stationary to the ground. The orientation is that one of the vertical faces is pointed due North, with the three other vertical faces pointed South, East and West respectively.

In the first step, the Assassins intend match the train's Northbound velocity, while traveling on a parallel track in a handcar, and line up the crate with the window. In the second step, they launch the crate Eastwards at ~0.577c (velocity relative to the handcar).

For an observer stationary to the ground, the crate will be traveling at ~0.70711c with motion at an azimuth angle of 45°

Why won't a line drawn between the South Western edge of the crate and North Eastern edge of the crate have an azimuth angle of 45°, according to an observer that is stationary to the ground, once the launch sequence is complete?

Also, would reversing the order of adding velocity to the crate change the outcome (Handcar Eastwards at 0.5c then crate launched Northwards at ~0.577c)?

 

[Orodruin]

If the scenarios are different, then it has to do with differences in the crate's launch conditions, but what those differences are has not been well explained (At least not well enough for me to have a good understanding of why these are two different scenarios)

What is not clear in this description?

The point is that Alice’s box is launched with a Lorentz boost such that the north/south sides were perpendicular to the north/south direction before the boost. Bob’s box is instead launched from an orientation such that those sides are perpendicular to the north/south orientation after the boost.

 

[PeroK]

I've thought about this, but I'm not sure how it will come into play and allow the box to pass through the window. I'd really appreciate you read the whole thing and provide a clear resolution if you can. Thanks

Others have done that. I don't like long narratives that inevitably hide key details in elaborate descriptions. Physics is about events with well-defined coordinates in a given frame of reference. If you specify your frame of reference and coordinates of every event then transform to any other frame correctly, then there are no paradoxes and all is clear.

 

[PeroK]

Let's consider a more well defined launch scenario:

The assassins intend to launch the crate in a two step process, with each of the faces starting at an initial orientation, while stationary to the ground. The orientation is that one of the vertical faces is pointed due North, with the three other vertical faces pointed South, East and West respectively.

In the first step, the Assassins intend match the train's Northbound velocity, while traveling on a parallel track in a handcar, and line up the crate with the window.

So, we may as well move to the train frame at this stage. In which the train and hancar are stationary.

In the second step, they launch the crate Eastwards at ~0.577c (velocity relative to the handcar).

Let's take the crate's velocity to be in the $x$ direction.

For an observer stationary to the ground, the crate will be traveling at ~0.70711c with motion at an azimuth angle of 45°

It's better to do a full position and velocity transformation from the train-handcar frame to the ground frame here. The crate has four corners, each of which has an initial position in the train-handcar frame and begins moving simultaneously in this frame.

One problem is that the corners of the crate begin moving at different times in the ground frame. The bottom two corners move simultaneously, but before the top two corners. I think this has been simulated in previous posts.

Why won't a line drawn between the South Western edge of the crate and North Eastern edge of the crate have an azimuth angle of 45°, according to an observer that is stationary to the ground, once the launch sequence is complete?

Because of the relativity of simultaneity. The different corners are launched at different times in the ground frame. The bottom corners first, then the top corners. The edges remain straight lines in the ground frame.

Also, would reversing the order of adding velocity to the crate change the outcome (Handcar Eastwards at 0.5c then crate launched Northwards at ~0.577c)?

It would change things, in the sense that the relativity of simulatenity would apply differently. In this case, the rear (westward) corners would be launched first, then the front (eastward) corners.

 

[Gamma Anon]

What is not clear in this description?

Yes it is clear.

But as expressed in my most recent post, a two step boost seems to allow for the crate's initial orientation to be as Alice assumed, but for the outcome to be as Bob predicts.

It's confusing, that a two step boost would have a different outcome to a one step boost, but maybe I'm wrong about that.

Your thoughts would be greatly appreciated.

 

[PeroK]

It's confusing, that a two step boost would have a different outcome to a one step boost, but maybe I'm wrong about that.

It's called a Wigner Rotation and it's a fundamental insight into the nature of spacetime. In mathematical terms, boosts do not form a sub-group of the Lorentz group of boosts and rotations. I.e. the composition of two boosts will be (in general) a boost plus a rotation.

https://en.wikipedia.org/wiki/Wigner_rotation

 

[Orodruin]

Ok, so to just look at what happens in the scenario that Bob describes. In the train's rest frame in Bob's scenario, we have the following situation:

Here, the crate is traveling straight at the window with at speed $v$ and with the sides parallel to the train. The world lines of the points 1-3 can be described by
$$
x_1 = vt_1, \quad y_1 = 0, \quad x_2 = vt_2 + \frac \ell{\gamma_v}, \quad y_2 = 0, \quad x_3 = vt_3, \quad y_3 = \ell.
$$
Lorentz transforming to the ground frame, traveling at speed $u$ relative to the train, and evaluating at the same time $t' = 0$ results in
$$
(x_1', y_1') = (0,0), \quad (x_2',y_2') = (\ell/\gamma_v,0), \quad (x_3', y_3') = (-uv\ell, \ell/\gamma_u).
$$
We therefore have the following situation in the ground frame:

It is clear that this is not the same situation that is obtained from just boosting the crate from an orientation parallel to the train as described by Alice. Instead, it is something that is obtained by boosting a rotated crate. In the situation described in the OP, where the boost is at velocity $1/\sqrt{2}$ at an angle of $\pi/4$, we can find the required rotation angle geometrically:

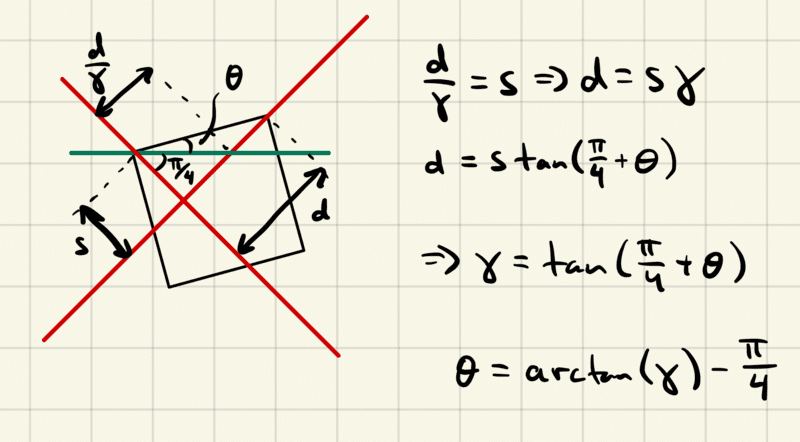
Here, the red lines are the directions parallel/orthogonal to the boost. The contraction occurs along the line tilted to the NE/SW and we require the top black line to contract into the green line. This means that the contraction along the boost direction must be given by $\gamma = \tan(\pi/4 + \theta)$ where $\theta$ is the rotation angle before the boost. Solving for $\theta$ gives $\theta = \tan^{-1}(\gamma) - \pi/4$. In particular, if $v = 1/\sqrt{2}$ then $\gamma = 1/\sqrt{1-1/2} = \sqrt{2}$ and so $\theta = \tan^{-1}(\sqrt 2) - \pi/4$. This corresponds to a rotation of $\theta \simeq 10^\circ$.

 

[Orodruin]

Also, here is the rotated box (black) with the boosted box (green):

This was constructed by contracting in the direction of the velocity until the upper/lower faces became horizontal.

Edit: Note that the black box is how the box will appear in the rest frame of the box under the assumption that we take the rest frame that is a pure boost from the ground frame (which is differs by a rotation from that obtained by consecutive boosts in the x and y directions due to Wigner rotation).

Edit 2: Conclusion: If I am the criminal mastermind plotting this deed then Alice better listen to Bob.

 

[Orodruin]

But as expressed in my most recent post, a two step boost seems to allow for the crate's initial orientation to be as Alice assumed, but for the outcome to be as Bob predicts.

It's confusing, that a two step boost would have a different outcome to a one step boost, but maybe I'm wrong about that.

A two step boost is not a pure boost but a boost plus a rotation so it would not be equivalent to a single step boost. This rotation is known as a Wigner rotation as mentioned earlier in the thread.

 

[PeroK]

A two step boost is not a pure boost but a boost plus a rotation so it would not be equivalent to a single step boost. This rotation is known as a Wigner rotation as mentioned earlier in the thread.

@Gamma Anon

One of the things that makes SR potentially tricky is that some things are not transitive that we intuitively expect to be.

In this case $B$ is moving along the x-axis relative to $A$, who share a common set of Cartesian coordinate axes (in the sense that the axes' directions spatially coincide in both frames at $t_A = t_B = 0$).

We also have $C$ moving along the y-axis relative to $B$. Likewise, $B$ and $C$ share a common set of coordinate axes (again in the sense that the axes' directions spatially coincide in both frames at $t_B = t_C = 0$).

And, yet, $A$ and $C$ do not share a set of Cartesian coordinate axes. At $t_A = t_C = 0$ when the origin of all three reference frames coincide, $C$'s axes (as measured by $A$) are rotated and not orthogonal. And vice versa.

 

[Dale]

I've done the math

No, you haven’t. You have guessed at the math. Doing the math entails doing what @Nugatory described and what I actually calculated. If you had done the math you would see that the assassins do have a shot according to the ground frame, contrary to Alice’s reasoning.

While this line will be shortened

That isn’t the important line to consider.

Here is the problem with that: Alice is considering one specific orientation of the crate and saying that that orientation will not work. Bob would agree that orientation would not work. Bob’s analysis finds a different orientation that does work. In Bob’s frame that orientation is easy to find, he knows that any other orientation will fail so he describes the one orientation of the box that the assassins can use that will succeed. My analysis shows that in the ground frame that orientation does indeed work also.

The fact that there exist orientations, like Alice’s, that don’t work is irrelevant. There exists one orientation that does. Therefore the assassins do have a shot. Alice is wrong because she took your “easy analysis” approach and assumed she knew the answer without doing the hard math.

 

[Dale]

If you specify your frame of reference and coordinates of every event then transform to any other frame correctly, then there are no paradoxes and all is clear.

This! @Gamma Anon pay attention to this.

The train frame is clear and easy to specify everything. From there you can transform to the ground frame or the box frame.

It's confusing, that a two step boost would have a different outcome to a one step boost, but maybe I'm wrong about that.

Your thoughts would be greatly appreciated.

As I mentioned earlier, the boosts do not form a group. A pair of non-colinear boosts is not a boost but a rotation and a boost

 

[Orodruin]

The train frame is clear and easy to specify everything. From there you can transform to the ground frame or the box frame.

Just to point out: This was done in #42.

 

[Orodruin]

Conclusion: If I am the criminal mastermind plotting this deed then Alice better listen to Bob.

Side note: This should be expected ... Dr. Mount Doom. Supervillain right there.

 

[Gamma Anon]

Hats off to Orodruin for the thorough explanation. Greatly Appreciated

My difficulty in immediately understanding the distinct differences between the outcomes expected by Bob and Alice, came from not understanding how a two boost approach (North then East) is distinctly different from a single boost approach (North East). Apologies for that.

Because under a two boost approach the crate begins with all the vertical faces pointed in cardinal directions, I thought that once the launch was completed, the crate would be observed with the same orientation by a ground observer, as if it had been launched at the window by a single boost at the same orientation.

Clearly a big issue with my understanding of Wigner Rotation. More reading ahead of me.

 

[Sagittarius A-Star]

Edit 2: Conclusion: If I am the criminal mastermind plotting this deed then Alice better listen to Bob.

I thought it would be easier for Alice to throw a sphere (with radius $R$) instead of a crate, that fits through the window, with speed $\frac{c}{\sqrt{2}}$ at 45°. But now I am not sure.

By length contraction it becomes an ellipsoid:
$a=R$
$b=R/\gamma(\frac{c}{\sqrt{2}}) = R \frac{\sqrt{2}}{2}$.

$x(\varphi) = R \cos(\varphi)$
$y(\varphi) = R \frac{\sqrt{2}}{2} \sin(\varphi)$

$d = \sqrt{x(135°)^2+y(135°)^2}=R \frac{\sqrt{3}}{2}$

The result for d has the vertical component of the length contraction of the sphere, which fits to the length contraction factor of the window, moving at $\frac{c}{2}$. But this cannot go through the window, because in the ground frame, the sphere must touch the "South" edge of the window earlier than the "North" edge. Reason: Relativity of simultaneity.

My conclusion would be, that Alice is in this case not allowed to use a 45° angle.

Am I correct?

 

[Dale]

I thought it would be easier for Alice to throw a sphere (with radius R) instead of a crate, that fits through the window, with speed c2 at 45°. But now I am not sure.

Look at it in the train frame. If it can fit in the train frame then it can fit in the ground frame too. Just describe it fully in the train frame and then transform to the ground frame.

 

[Sagittarius A-Star]

Look at it in the train frame. If it can fit in the train frame then it can fit in the ground frame too. Just describe it fully in the train frame and then transform to the ground frame.

In the train frame it must fit through the window. Then there must be an error in my calculation.

 

[Orodruin]

$x(\varphi) = R \cos(\varphi)$
$y(\varphi) = R \frac{\sqrt{2}}{2} \sin(\varphi)$

$d = \sqrt{x(135°)^2+y(135°)^2}=R \frac{\sqrt{3}}{2}$

You have an arithmetic error here somewhere. Considering that $R/\sqrt{2} < R$, it follows that
$$
d = R\sqrt{ \cos^2(\varphi) + \sin^2(\varphi)/2} \leq R \sqrt{\cos^2(\varphi) + \sin^2(\varphi)} = R.
$$
You therefore clearly cannot get a result larger than $R$.

That the ball will fit through the window is clear from the fact that it can be inscribed in the box and we know that the box will go through if oriented correctly.

 

[Sagittarius A-Star]

You therefore clearly cannot get a result larger than $R$.

My $d = R \frac{\sqrt{3}}{2}$ is smaller than $R$. The window is length contracted by the same factor. But there must be an arithmetical error.

 

[Orodruin]

My $d = R \frac{\sqrt{3}}{2}$ is smaller than $R$. The window is length contracted by the same factor. But there must be an arithmetical error.

Yes, that was clearly a brain fart on my part. Ok, new try: The argument 135 degrees does not correspond to the line d that you drew. It is the vertical line in the circle rest frame but is tilted in the ground rest frame. This probably has something to do with the resolution. You need the point on the ellipse with the largest vertical projection.

 

[Orodruin]

The vertical projection is $-\cos(\varphi)/\sqrt 2 + \sin(\varphi)/2$ (I normalized R to one). This has amplitude $\sqrt 3/2$, same as the length contraction of the window. Hence, no problem.

 

[jartsa]

The question is not whether Alice and Bob know about Wigner rotation. The question is if the assassins do. If they do then they can make the plot work by launching the box in the appropriate orientation. If they don’t, they will fail. So whether Alice or Bob will be right will depend on the assassins’ knowledge of relativity.

Oh yes, Alice and Bob were police people, not assassins. The story has too many characters for me to follow.

 

[Sagittarius A-Star]

Yes, that was clearly a brain fart on my part. Ok, new try: The argument 135 degrees does not correspond to the line d that you drew. It is the vertical line in the circle rest frame but is tilted in the ground rest frame. This probably has something to do with the resolution. You need the point on the ellipse with the largest vertical projection.

I think I found my error (after a long time). It has nothing to do with relativistic effects, because I calculated only in the ground frame. I simply wrote wrong formulas for an ellipse.

Contains wrong formulas:

$a=R$
$b=R/\gamma(\frac{c}{\sqrt{2}}) = R \frac{\sqrt{2}}{2}$.

$x(\varphi) = R \cos(\varphi)$
$y(\varphi) = R \frac{\sqrt{2}}{2} \sin(\varphi)$

$d = \sqrt{x(135°)^2+y(135°)^2}=R \frac{\sqrt{3}}{2}$

Correct formulas:

$(x, y) = (a \cos(t), b \sin(t))\ \ \ \ \$ Here $0 \leq t \leq 2\pi$ is a parameter, but not the angle to a point on the elipse.

Polar form relative to center:
$r(\varphi) = \frac{ab}{\sqrt{((b \cos(\varphi))^2 + ((a \sin(\varphi))^2}}$

Source:
https://en.wikipedia.org/wiki/Ellipse#Polar_form_relative_to_center

 

[Orodruin]

I think I found my error (after a long time). It has nothing to do with relativistic effects, because I calculated only in the ground frame. I simply wrote wrong formulas for an ellipse.

Contains wrong formulas:Correct formulas:

$(x, y) = (a \cos(t), b \sin(t))\ \ \ \ \$ Here $0 \leq t \leq 2\pi$ is a parameter, but not the angle to a point on the elipse.

Polar form relative to center:
$r(\varphi) = \frac{ab}{\sqrt{((b \cos(\varphi))^2 + ((a \sin(\varphi))^2}}$

Source:
https://en.wikipedia.org/wiki/Ellipse#Polar_form_relative_to_center

As I said earlier, there is nothing really wrong with the formulas. The wrong assumption is that the angle $\varphi = 135^\circ$ corresponds to the vertical line. This is true only in the rest frame of the ellipse.