The physics of the inclined pushup

[Wes Turner]

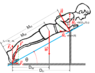
I am trying to analyze the physics of the inclined pushup. I have attached a PDF showing what I have so far. I would appreciate any critiques. I don't see the attachment in the preview, so I hope it is visible.

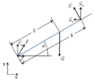
I am especially concerned with Figure 5. I have placed the load (W) at the center of mass and separated the components. I then adjusted Ws, the weight in the direction of the force applied by the arms at the shoulders by the mechanical advantage to get Fs, the force needed to raise the body.

Is this all correct?

Thanks

 

[Orodruin]

First of all, a correctly performed push-up does not have the hands at the level of the shoulders. Particularly not in the bottom position. See, e.g., from 4.32 of this video:

At the top of the pushup, your hands might be essentially below your shoulders due to your shoulders moving in a circle and therefore backwards, but it should not be the setup in the bottom position and the angle between your arms and your body will be less than 90 degrees in the top position.

Another effect that you seem to be neglecting is the fact that the centre of mass of your body will typically be behind your toes (which you are standing on). This will affect the moment arm of your centre of mass and thereby the moment that your hands pushing will need to generate to lift you.

I suggest you look at the force that needs to be generated by your hands on the ground rather than the force on the shoulders. At the shoulders relative to the arms there will be many forces acting, inducing torques around the shoulders in order to let the hands generate the appropriate amount of force.

 

[Wes Turner]

First of all, a correctly performed push-up does not have the hands at the level of the shoulders. Particularly not in the bottom position. See, e.g., from 4.32 of this video:

At the top of the pushup, your hands might be essentially below your shoulders due to your shoulders moving in a circle and therefore backwards, but it should not be the setup in the bottom position and the angle between your arms and your body will be less than 90 degrees in the top position.

Great video, thanks for that.

Yes, I know that the hands are not exactly below the shoulders, but I thought it would be close enough for what I am trying to do. How much difference would there be between the hands being exactly below the shoulders and a few inches lower? How would I go about calculating that difference?

Another effect that you seem to be neglecting is the fact that the centre of mass of your body will typically be behind your toes (which you are standing on). This will affect the moment arm of your centre of mass and thereby the moment that your hands pushing will need to generate to lift you.

I don't understand this. I thought the center of mass of anybody is a fixed property of that body. In the own position, which is where I am doing my calculations, the body is at rest supported by the toes and hands. Can you provide a sketch showing that the center of behind the toes?

I suggest you look at the force that needs to be generated by your hands on the ground rather than the force on the shoulders. At the shoulders relative to the arms there will be many forces acting, inducing torques around the shoulders in order to let the hands generate the appropriate amount of force.

I guess that was what I was trying to do. I might have just drawn the Fp arrow in the wrong place. I was trying to calculate the force on the hands of the weight of the body reduced by the mechanical advantage of the lever.

 

[tnich]

I like your presentation. I only have one minor quibble. You correctly define $W_F= W \sin \theta$ to be a force parallel to the body, but subsequently refer to it as "weight on the feet". When the body is parallel to the ground, the weight on the feet is $W(1-\frac c s)$. In general, using your diagram and assumptions, the weight supported by the feet would be $W(1-\frac c s \cos^2 \theta)$, and the total force exerted by the feet $W(1-\frac c s)\cos \theta$.

 

[Orodruin]

Yes, I know that the hands are not exactly below the shoulders, but I thought it would be close enough for what I am trying to do. How much difference would there be between the hands being exactly below the shoulders and a few inches lower? How would I go about calculating that difference?

I would say that on an adult the difference would amount to something around 10-15 cm. This would be a difference of around 6-10% in the moment arm relative to the feet.

I don't understand this. I thought the center of mass of anybody is a fixed property of that body. In the own position, which is where I am doing my calculations, the body is at rest supported by the toes and hands. Can you provide a sketch showing that the center of behind the toes?

As long as that body does not change shape or weight distribution. It is quite easy to understand that the CoM is behind the toes in the straight position. If it was not you would be constantly at risk of falling over when standing straight. You can see that it changes the moment arm from your figure 5. Imagine tilting the push-uper even more up. If the CoM was not behind the toes then he would reach equilibrium only at the very last moment. Imagine replacing the man by a long homogeneous box - you do not need to get the box to a fully upright position for the CoM to be above the contact point with the ground. The same principle applies here.

So here is a fun additional task: Argue for why push-ups are easier when standing on your knees.

 

[Wes Turner]

I like your presentation. I only have one minor quibble. You correctly define $W_F= W \sin \theta$ to be a force parallel to the body, but subsequently refer to it as "weight on the feet". When the body is parallel to the ground, the weight on the feet is $W(1-\frac c s)$. In general, using your diagram and assumptions, the weight supported by the feet would be $W(1-\frac c s \cos^2 \theta)$, and the total force exerted by the feet $W(1-\frac c s)\cos \theta$.

Did you come up with the equation for the weight felt by the feet by first calculating the weight felt by the hands ($W(\frac c s)$) and then subtracting that from W?

The attached diagram illustrates this. Is it correct? It makes intuitive sense. If I set S=C (moving the hands/shoulders to the center of mass), then the weight felt by the hand = W and the weight felt by the feet = 0, which is as it should be. Similarly, if I set S=H (move the hands to the top of the head), then both the hands and feet feel a weight of W/2.

 

[tnich]

Did you come up with the equation for the weight felt by the feet by first calculating the weight felt by the hands ($W(\frac c s)$) and then subtracting that from W?

Yes.

The attached diagram illustrates this. Is it correct? It makes intuitive sense. If I set S=C (moving the hands/shoulders to the center of mass), then the weight felt by the hand = W and the weight felt by the feet = 0, which is as it should be. Similarly, if I set S=H (move the hands to the top of the head), then both the hands and feet feel a weight of W/2.

If you draw a similar free body diagram for the inclined push-up, you can solve the resulting force and torque equations for the force exerted by the feet. I did find an error in my solution, though. The total force exerted by the feet should be
$W \sqrt{1 - 2\frac c s \cos^2 \theta + (\frac c s)^2 \cos^2 \theta}$

 

[Wes Turner]

Yes.

OK

If you draw a similar free body diagram for the inclined push-up, you can solve the resulting force and torque equations for the force exerted by the feet.

Here's the drawing, but I don't think I have the forces correct. The force at the shoulder/hands (=WhCos(θ)) looks reasonable, but I don't know what to do with the other forces. Do I break W up into components like Wh and then set Wt = W - WhCos(θ) - WCos(θ)?

I did find an error in my solution, though. The total force exerted by the feet should be
$W \sqrt{1 - 2\frac c s \cos^2 \theta + (\frac c s)^2 \cos^2 \theta}$

I don't follow that at all. Can you provide a diagram?

 

[tnich]

OK

Here's the drawing, but I don't think I have the forces correct. The force at the shoulder/hands (=WhCos(θ)) looks reasonable, but I don't know what to do with the other forces. Do I break W up into components like Wh and then set Wt = W - WhCos(θ) - WCos(θ)?

Your free body diagram does not show all of the forces. The first thing you need to decide is, what is the (single) object that the forces act on. (In more complex problems with multiple objects, you may need to draw a FBD for each one.) In this case you have one object - the person doing the pushups. I have drawn this as a blue line in my diagram. This assumes that all of the forces act on points on the same line, which is an approximation.

This diagram shows all of the forces acting on the body - the force on the center of gravity $\vec W$, the force on the shoulders $\vec S$, and the force on the feet $\vec F$.

I am assuming the object is not moving (yet), so the net force and the net torque should be zero. Using those facts and the diagram, you should be able write the equations for the net force in both the x direction and the y direction, and for the net torque.

Notice that to get a net force of zero in the x direction, you a need a force to balance $\vec N_x$. The only place this force can be exerted is on the feet. So
$0 = \vec N_x + \vec F_x$

I point this out to show that using the FBD and the net force/torque equations together, you can usually figure out what all of the forces are and in which directions they act.

I don't follow that at all. Can you provide a diagram?

Using this diagram, you should be able to write out the net torque/force equations and solve for $|\vec F|$.

 

[Wes Turner]

Hi, I am just getting back to this after cleaning up some more pressing work.

This diagram shows all of the forces acting on the body - the force on the center of gravity $\vec W$, the force on the shoulders $\vec S$, and the force on the feet $\vec F$.

A couple of questions:

1. I do not see any force labeled $\vec S$ in your diagram. Did you mean $\vec N$ or should there be another down arrow at the shoulders labelled $\vec S$?
2. The forces at the shoulders are all labeled $\vec N$. Are these the Normal forces exerted by support surface where the person is resting their hands?
3. The forces at the feet are all labeled $\vec F$. Are these not also Normal forces? Should they be labeled something like $\vec N_f$, $\vec N_{fx}$, and $\vec N_{fy}$? And if so, then the Normal forces at the shoulders also need an extra subscript, something like $\vec N_s$, $\vec N_{sx}$, and $\vec N_{sy}$, no?
   
4. The force at the feet labeled $\vec F$ is pointing at what appears to be an angle of $\Theta$ above the body line. Is that correct? How did you arrive at that angle? Does that mean that the feet are exerting an equal and opposite force on the ground?

Notice that to get a net force of zero in the x direction, you a need a force to balance $\vec N_x$. The only place this force can be exerted is on the feet. So
$0 = \vec N_x + \vec F_x$

Do you mean on the feet or by the feet? If it's on the feet, what is exerting that force?

Do we also need a force to balance $\vec N_y$ or are the two y forces Normal forces exerted by the floor and the elevated support?

 

[tnich]

Hi, I am just getting back to this after cleaning up some more pressing work.

A couple of questions:

1. I do not see any force labeled $\vec S$ in your diagram. Did you mean $\vec N$ or should there be another down arrow at the shoulders labelled $\vec S$?
2. The forces at the shoulders are all labeled $\vec N$. Are these the Normal forces exerted by support surface where the person is resting their hands?
3. The forces at the feet are all labeled $\vec F$. Are these not also Normal forces? Should they be labeled something like $\vec N_f$, $\vec N_{fx}$, and $\vec N_{fy}$? And if so, then the Normal forces at the shoulders also need an extra subscript, something like $\vec N_s$, $\vec N_{sx}$, and $\vec N_{sy}$, no?
   
4. The force at the feet labeled $\vec F$ is pointing at what appears to be an angle of $\Theta$ above the body line. Is that correct? How did you arrive at that angle? Does that mean that the feet are exerting an equal and opposite force on the ground?

Do you mean on the feet or by the feet? If it's on the feet, what is exerting that force?

Do we also need a force to balance $\vec N_y$ or are the two y forces Normal forces exerted by the floor and the elevated support?

You are right, there is no $\vec S$ in the diagram. I called it $\vec N$ in the diagram.
The answer to the rest of your questions is that each force has an equal and opposite opposing force. The weight on the hands and feet would add up to $\vec W$. But since I already have $\vec W$ in the diagram, putting vectors for weight on the shoulders and feet would be double counting. As it is, the diagram shows each force once, with the forces on the shoulders and feet broken out into x and y components. Everything else can be derived from what is shown in the diagram, including the angle of $\vec F$. Try using the diagram to write the equations for net forces in the x and y directions.

 

[tnich]

You are right, there is no $\vec S$ in the diagram. I called it $\vec N$ in the diagram.
The answer to the rest of your questions is that each force has an equal and opposite opposing force. The weight on the hands and feet would add up to $\vec W$. But since I already have $\vec W$ in the diagram, putting vectors for weight on the shoulders and feet would be double counting. As it is, the diagram shows each force once, with the forces on the shoulders and feet broken out into x and y components. Everything else can be derived from what is shown in the diagram, including the angle of $\vec F$. Try using the diagram to write the equations for net forces in the x and y directions.

Oh, and the net torque equation.

 

[tnich]

Oh, and the net torque equation.

One of the key concepts you need to draw a free body diagram is that you need to decide what body it represents. In this case it is the body of the person doing the pushups, not the things he is pushing against. In the diagram you only include the forces acting on that body, not reaction forces. In this case, there are only three forces acting on the body - the force of gravity $\vec W$ acting downward, the normal force at the shoulders $\vec N$, and the force on the feet $\vec F$.

 

[Wes Turner]

One of the key concepts you need to draw a free body diagram is that you need to decide what body it represents. In this case it is the body of the person doing the pushups, not the things he is pushing against. In the diagram you only include the forces acting on that body, not reaction forces. In this case, there are only three forces acting on the body - the force of gravity $\vec W$ acting downward, the normal force at the shoulders $\vec N$, and the force on the feet $\vec F$.

This was very helpful. I see now that I was getting myself confused by having forces acting all over the place.

Let me start over with the forces in the down position. Consider this diagram. I am using an actual person image, rather than a blue line, because I am writing this for normal (non-techie) people.

C and S are as before, the distances to the center of mass and the shoulders. D is the distance to the support structure where the hands are placed. Here it is the same as S, but when we raise the hands, it will be shorter.

I have three forces, $\vec N_f$, the normal force at the feet, $\vec W$, the weight of the body, and $\vec N_s$, the normal force applied at the shoulders.

I am happy with the first two, but $\vec N_s$ bothers me. I have labeled it as being applied at the shoulders, but I show it being applied at the hands, which are located slightly below the shoulders.

Should I rename it $\vec N_h$, the normal force applied at the hands? In that case, what is the moment arm? Is it the distance from the feet to the hands or the feet to the shoulders? I have been using the shoulders. And if it's to the shoulders, do I need to do another moment arm correction between the hands and the shoulders?

On me, the difference is only about 2 inches, so I am inclined to rename it $\vec N_h$ and ignore the small difference between the hands and the shoulders. I want to keep this as simple as possible. I am not designing components for a supersonic jet. I'm just trying to get a good general sense of the weight the person will need to be able to lift at different elevations.

Suggestions?

 

[tnich]

This was very helpful. I see now that I was getting myself confused by having forces acting all over the place.

Let me start over with the forces in the down position. Consider this diagram. I am using an actual person image, rather than a blue line, because I am writing this for normal (non-techie) people.
View attachment 230196
C and S are as before, the distances to the center of mass and the shoulders. D is the distance to the support structure where the hands are placed. Here it is the same as S, but when we raise the hands, it will be shorter.

I have three forces, $\vec N_f$, the normal force at the feet, $\vec W$, the weight of the body, and $\vec N_s$, the normal force applied at the shoulders.

I am happy with the first two, but $\vec N_s$ bothers me. I have labeled it as being applied at the shoulders, but I show it being applied at the hands, which are located slightly below the shoulders.

Should I rename it $\vec N_h$, the normal force applied at the hands? In that case, what is the moment arm? Is it the distance from the feet to the hands or the feet to the shoulders? I have been using the shoulders. And if it's to the shoulders, do I need to do another moment arm correction between the hands and the shoulders?

On me, the difference is only about 2 inches, so I am inclined to rename it $\vec N_h$ and ignore the small difference between the hands and the shoulders. I want to keep this as simple as possible. I am not designing components for a supersonic jet. I'm just trying to get a good general sense of the weight the person will need to be able to lift at different elevations.

Suggestions?

A couple of suggestions.
1) Stick with the force on the hands and do not show the force on the shoulders. If you are considering the body to include the arms and hands, then you have a normal force acting on the hands and the distance D will be the same throughout the execution of the pushup. If not, then you have lateral forces acting on the shoulders that you probably don't want to consider.
2) Use force labels that will also be appropriate for the inclined position. The normal force on the hands should work for both the horizontal and inclined positions. The force on the feet will not be normal in the inclined position.

 

[A.T.]

View attachment 230196

Should I rename it $\vec N_h$, the normal force applied at the hands? In that case, what is the moment arm? Is it the distance from the feet to the hands or the feet to the shoulders?

The external force is at the hands, so feet to hands is the relevant lever arm for the external moment balance around the foot contact. The shoulder position is relevant for the moment balance around the shoulder joint (shoulder muscles vs. external force at hands).

 

[Wes Turner]

A couple of suggestions.
1) Stick with the force on the hands and do not show the force on the shoulders. If you are considering the body to include the arms and hands, then you have a normal force acting on the hands and the distance D will be the same throughout the execution of the pushup. If not, then you have lateral forces acting on the shoulders that you probably don't want to consider.

Great, thanks.

2) Use force labels that will also be appropriate for the inclined position. The normal force on the hands should work for both the horizontal and inclined positions. The force on the feet will not be normal in the inclined position.

I don't understand.

In your FBD, you show $\vec N$, which I assume is the normal force. But it is not orthogonal to the ground, which is what is needed to oppose gravity, no? Are normal forces always orthogonal to the body they are acting on?

If the force on the feet in the inclined position is not normal, then what is it? What is $\vec F$ in your FBD? Is it friction? Is that why you labeled it "F" and I just assumed it meant "feet"? And if so, then is there no normal force on the feet? Or is it $\vec F_y$, but that is not orthogonal to the body either.

This may be too complicated for my feeble brain...

 

[tnich]

In your FBD, you show $\vec N$, which I assume is the normal force. But it is not orthogonal to the ground, which is what is needed to oppose gravity, no? Are normal forces always orthogonal to the body they are acting on?

If the force on the feet in the inclined position is not normal, then what is it? What is $\vec F$ in your FBD? Is it friction? Is that why you labeled it "F" and I just assumed it meant "feet"? And if so, then is there no normal force on the feet? Or is it $\vec F_y$, but that is not orthogonal to the body either.

This may be too complicated for my feeble brain...

A normal force is normal to the surface that applies the force. So if the person doing the pushups is leaning against a surface, the normal force is the force of the surface on the hands that is normal to the surface. In the case of the feet, if the feet rest on the floor, then the normal force would be perpendicular to the floor. The horizontal force on the feet would be due to friction. To keep the body from moving horizontally, there needs to be an equal and opposite force to counter the horizontal force on the hands. So to calculate it, you would just change the sign of the horizontal component of the normal force on the hands.

This all assumes that the force on the hands is a normal force. That is, that the person doing the pushups is not using friction of the surface to keep from sliding along it. That seems like a reasonable assumption, but it is not a necessary one.

 

[Wes Turner]

A normal force is normal to the surface that applies the force.

And "normal" means orthogonal or perpendicular, right?

So if the person doing the pushups is leaning against a surface, the normal force is the force of the surface on the hands that is normal to the surface. In the case of the feet, if the feet rest on the floor, then the normal force would be perpendicular to the floor.

Where on your FBD is the normal force on the feet? Is it $\vec F_y$?

The horizontal force on the feet would be due to friction. To keep the body from moving horizontally, there needs to be an equal and opposite force to counter the horizontal force on the hands. So to calculate it, you would just change the sign of the horizontal component of the normal force on the hands.

This all assumes that the force on the hands is a normal force. That is, that the person doing the pushups is not using friction of the surface to keep from sliding along it. That seems like a reasonable assumption, but it is not a necessary one.

OK, I think I have it. In your FBD, $\vec F_y$ is the normal force on the feet that keeps them from falling through the floor due to gravity. $\vec F_x$ is the frictional force that counteracts (balances) $\vec N_x$, the x- component of the inclined normal force on the hands. And $\vec F$ is just the combination of $\vec F_y$ & $\vec F_x$. Right?

I got confused because at the hands (formerly shoulders), we started with $\vec N$ and broke it into x and y components. At the feet, we worked the other way around. We started with the components and constructed $\vec F$. Or at least that's how I viewed it.

As you say, I have $\vec F_x$. It's just the opposite of $\vec N_x$. For my purposes, I really don't need $\vec F_y$, unless that's how I get to $\vec N$, which is what I am interested in.

I believe that $\vec W = -\vec F_y - \vec N_y$ for all $\theta$. Correct?

I think I can calculate $\vec N_y$ at any inclination angle from the standard equations of a lever, as I did for the down position. As the angle increases, $\vec N_y$ will decrease to zero and $\vec F_y$ will increase to $-\vec W$ and they will always add up to $-\vec W$. Right?

So, unless you see some errors in the above, I will do that work and come back with my results.

Cheers...

 

[Wes Turner]

One more question. You mentioned that it would be good if I could choose variable names that could be consistent and meaningful both in the down and inclined positions. What if I call the forces in the down position $\vec N_F$ & $\vec N_H$?

When I incline it, $\vec N_F$ will become what you call $\vec F_y$ and will always point straight up. $\vec N_H$ will become what you call $\vec N$ and will be normal to the plane of the body. I can break $\vec N_H$ up into $\vec N_Hx$ & $\vec N_Hy$. I'm not sure what to call the components of $\vec N_F$, maybe $\vec F_Fx$ & $\vec F_F$?

Thanks

 

[tnich]

OK, I think I have it. In your FBD, $\vec F_y$ is the normal force on the feet that keeps them from falling through the floor due to gravity. $\vec F_x$ is the frictional force that counteracts (balances) $\vec N_x$, the x- component of the inclined normal force on the hands. And $\vec F$ is just the combination of $\vec F_y$ & $\vec F_x$. Right?

I got confused because at the hands (formerly shoulders), we started with $\vec N$ and broke it into x and y components. At the feet, we worked the other way around. We started with the components and constructed $\vec F$. Or at least that's how I viewed it.

As you say, I have $\vec F_x$. It's just the opposite of $\vec N_x$. For my purposes, I really don't need $\vec F_y$, unless that's how I get to $\vec N$, which is what I am interested in.

I believe that $\vec W = -\vec F_y - \vec N_y$ for all $\theta$. Correct?

I think I can calculate $\vec N_y$ at any inclination angle from the standard equations of a lever, as I did for the down position. As the angle increases, $\vec N_y$ will decrease to zero and $\vec F_y$ will increase to $-\vec W$ and they will always add up to $-\vec W$. Right?

So, unless you see some errors in the above, I will do that work and come back with my results.

Cheers...

This all looks correct.

One more question. You mentioned that it would be good if I could choose variable names that could be consistent and meaningful both in the down and inclined positions. What if I call the forces in the down position $\vec N_F$ & $\vec N_H$?
View attachment 230211
When I incline it, $\vec N_F$ will become what you call $\vec F_y$ and will always point straight up. $\vec N_H$ will become what you call $\vec N$ and will be normal to the plane of the body. I can break $\vec N_H$ up into $\vec N_Hx$ & $\vec N_Hy$. I'm not sure what to call the components of $\vec N_F$, maybe $\vec F_Fx$ & $\vec F_F$?

Thanks

I think it would be clearer to just choose a single letter for the force on the hands and another single letter for the force on the feet. Then you could use x and y subscripts to denote their horizontal and vertical components. Since the force on the feet is not purely a normal force anyway, there is no need to call it $\vec N_F$.

 

[Wes Turner]

I am starting to worry that I am in over my head here, but let me try one more time.

Here's my latest FBD for the down position:

$M_H$ & $M_W$ are the moment arms for the hands and weight. Using the standard equations for the lever, I get $H = W(M_W/M_H)$.

I then get $F=W(1-M_W/M_H)$.

I have added $D_W$ & $D_H$. They will replace $M_W$ & $M_H$ as the body is inclined. $M_W$ & $M_H$ will continue to measure the distances on the body, while $D_W$ & $D_H$ will be the projections of those measurements onto the floor.

Here's my new FBD for the inclined position:

I have $H_Y=W(D_W/D_H)$, using $D_W$ & $D_H$, the shorter projections of the moment arms onto the floor. Is that correct?

If so, then $H$, the parameter I care about, should be $H=H_Y*sin^{-1}(\theta)$.

Using that, I get $F_Y=W-H_Y$, but I'm not sure why I need that.Am I anywhere in the ballpark?

 

[tnich]

I am starting to worry that I am in over my head here, but let me try one more time.

Here's my latest FBD for the down position:
View attachment 230300
$M_H$ & $M_W$ are the moment arms for the hands and weight. Using the standard equations for the lever, I get $H = W(M_W/M_H)$.

I then get $F=W(1-M_W/M_H)$.

I have added $D_W$ & $D_H$. They will replace $M_W$ & $M_H$ as the body is inclined. $M_W$ & $M_H$ will continue to measure the distances on the body, while $D_W$ & $D_H$ will be the projections of those measurements onto the floor.
Here's my new FBD for the inclined position:
View attachment 230302
I have $H_Y=W(D_W/D_H)$, using $D_W$ & $D_H$, the shorter projections of the moment arms onto the floor. Is that correct?

This isn't quite right. Since we are assuming that the body is (initially) at rest, the net torque is zero. Torque is $\vec r \times \vec F$ where $\vec r$ is the vector from the reference point (in this case the feet) to the point where the force $\vec F$ is applied. The magnitude of the torque is $rF\sin\alpha$, where $\alpha$ is the angle between the two vectors if they are placed tail to tail. The net torque in this case is
$0 = \vec M_W \times \vec W + \vec M_H \times \vec H$

Then $M_WW\cos \theta = M_HH$ because $\theta =3\pi/2 - \alpha_W$.

If so, then $H$, the parameter I care about, should be $H=H_Y*sin^{-1}(\theta)$.

That should be $H=W\frac {M_W}{M_H}\cos \theta$.

Using that, I get $F_Y=W-H_Y$, but I'm not sure why I need that.

Am I anywhere in the ballpark?

You are doing well. You wanted the force on the feet. Now you $F_Y$ and you know how to get $F_X$. Put them together with the Pythagorean theorem, and you have $|F|$.

 

[A.T.]

Note that this assumes H is perpendicular to the bench.

 

[tnich]

Note that this assumes H is perpendicular to the bench.

Right, which is why the torque applied at the hands is $M_HH$. The force is perpendicular to the moment arm.