arcTomato
- 104
- 27
- Homework Statement
- Derive the power spectrum of sinusoid
- Relevant Equations
- descrete fourier transform
Hi
I would like to Derive the power spectrum of sinusoid.I tried like this. But It doesn't work.
<Moderator: CODE tags added>
When sinusoid frequancy is 7 and the sampling time series ##T=0.01s##, this is the power spectrum.
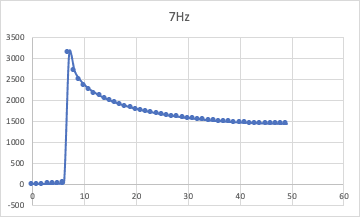 The paper I read says that "Only when the frequency of the sinusoid is equal to one of the Fourier frequencies will all power be concentrated in one bin of the discrete Fourier transform.", so I think the power spectrum should be delta function.
The paper I read says that "Only when the frequency of the sinusoid is equal to one of the Fourier frequencies will all power be concentrated in one bin of the discrete Fourier transform.", so I think the power spectrum should be delta function.
How can I derive the power spectrum as delta function?
Thank you.
I would like to Derive the power spectrum of sinusoid.I tried like this. But It doesn't work.
<Moderator: CODE tags added>
C:
#include <stdio.h>
#include <math.h>
#define pi 3.1415926535
FILE *in_file, *out_file;
int main()
{
dft();
}
int dft(int argc, char *argv[])
{
char *filename_in = argv[1];
char *filename_out = argv[2];
if(argc != 3){
printf("使い方: ./a.out <入力ファイル名> <出力ファイル名>\n");
return 0;
}
int j, k, N;
int max = 100000;
double f[max], re = 0, I am = 0;
if((in_file=fopen(filename_in,"r"))==NULL){
printf("in_file cannot open\n");
return 0;
}
for(N=0; N<max; N++) {
if(fscanf(in_file,"%lf", &f[N]) == EOF) break;
}
fclose(in_file);
if((out_file=fopen(filename_out,"w"))==NULL){
printf("outfile cannot open\n");
return 0;
}
//DFT part
for(j=(-N/2); j<N/2; j++) {
for(k=0; k<N; k++) {
re += f[k]*cos(2*pi*j*k/N);
I am += -f[k]*sin(2*pi*j*k/N);
}
fprintf(out_file,"%d, %f\n", j, re*re+im*im);
}
fclose(out_file);
return 0;
}How can I derive the power spectrum as delta function?
Thank you.
Last edited by a moderator:
 )
)