- #1
Whitehole
- 132
- 4
You are launched upward inside a railway coach in a horizontal position with respect to the surface of Earth, as shown in the figure. After the launch, but while the coach is still rising, you release two ball bearings at opposite ends of the train and at rest with respect to the train.
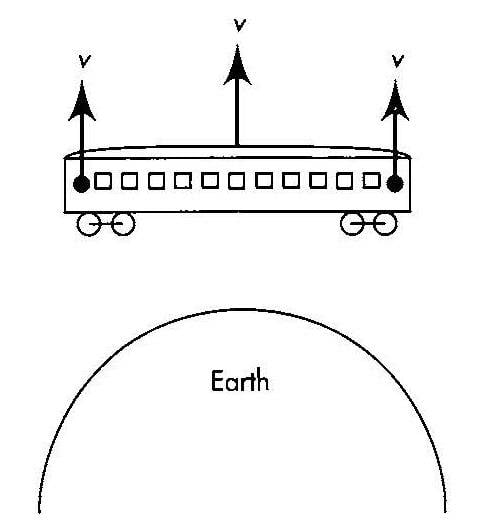
a) Riding inside the coach, will you observe the distance between the ball bearings to increase or decrease with time?
Answer: At the instant the coach was released, it is already starting to fall and since the objects inside the coach are also falling with the same rate with the coach, gravity is not present inside but just for a while. So, whether the coach is moving upwards or downwards doesn't really matter as long as they are falling at the same rate. Eventually tidal forces come into play so the distance between balls will increase during the upward trip.
b) Now you ride in a second railway coach launched upward in a vertical position with respect to the surface of Earth (not shown). Again you release two ball bearings at opposite ends of the coach and at rest with respect to the coach. Will you observe these ball bearings to move together or apart?
Answer: Again, at the instant the coach was released, it is already starting to fall. The two balls are experiencing approximately the same acceleration initially (lower ball has greater acceleration compared to the upper ball but just a tiny bit), but this tiny difference will cause a detectable change in separation between the balls as they fall. So, the two balls will move apart.
c) In either of the cases described above, can you, the rider in the railway coach, distinguish whether the coach is rising or falling with respect to the surface of Earth solely by observing the ball bearings from inside the coach? What do you observe at the moment the coach stops rising with respect to Earth and begins to fall?
Answer: No, because again as stated above, at the instant the coach was released, it is already starting to fall so whatever phenomena are observed inside when the coach is on the downward trajectory, it is the same phenomena during the upward trajectory. As the coach reaches the top of the trajectory, you still observe the same phenomena (signs of "non-inertial frame" if already exceeded the detection tolerance).
Can anyone please comment on my argument in this problem. Do I have the correct reasoning and intuition on the problem? Did I miss anything?
a) Riding inside the coach, will you observe the distance between the ball bearings to increase or decrease with time?
Answer: At the instant the coach was released, it is already starting to fall and since the objects inside the coach are also falling with the same rate with the coach, gravity is not present inside but just for a while. So, whether the coach is moving upwards or downwards doesn't really matter as long as they are falling at the same rate. Eventually tidal forces come into play so the distance between balls will increase during the upward trip.
b) Now you ride in a second railway coach launched upward in a vertical position with respect to the surface of Earth (not shown). Again you release two ball bearings at opposite ends of the coach and at rest with respect to the coach. Will you observe these ball bearings to move together or apart?
Answer: Again, at the instant the coach was released, it is already starting to fall. The two balls are experiencing approximately the same acceleration initially (lower ball has greater acceleration compared to the upper ball but just a tiny bit), but this tiny difference will cause a detectable change in separation between the balls as they fall. So, the two balls will move apart.
c) In either of the cases described above, can you, the rider in the railway coach, distinguish whether the coach is rising or falling with respect to the surface of Earth solely by observing the ball bearings from inside the coach? What do you observe at the moment the coach stops rising with respect to Earth and begins to fall?
Answer: No, because again as stated above, at the instant the coach was released, it is already starting to fall so whatever phenomena are observed inside when the coach is on the downward trajectory, it is the same phenomena during the upward trajectory. As the coach reaches the top of the trajectory, you still observe the same phenomena (signs of "non-inertial frame" if already exceeded the detection tolerance).
Can anyone please comment on my argument in this problem. Do I have the correct reasoning and intuition on the problem? Did I miss anything?