The slope of the tangent of the voltage curve.

[Samar A]

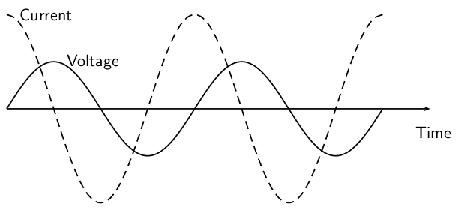
In an AC circuit with only a capacitor this diagram represents the relation between the current and the voltage in it (the current leads the voltage by 90 degrees).

and because: (I= dQ/dt) and ( Q=C*V)
where: Q is the amount of charge, C is the capacitance and V is the potential difference between the plates of the capacitor.
Then: I=C (dV/dt).
In the diagram above my textbook refers to the slope of the tangent of the voltage curve to be (dV/dt), and I don't understand it, could you please explain this for me? Regarding that I don't actually know how to determine the slope of a tangent of a curve.

 

[cnh1995]

Slope of the tangent at a point on the function is the derivative of the function at that point. It is a very big topic in calculus, called differential calculus.

Could you be more specific about what you don't understand in that graph?

 

[NascentOxygen]

Try: My textbook refers to the slope of the voltage versus time curve to be (dV/dt). To find this slope you draw a straight line that is tangential to the voltage curve, and the slope of this straight line is the slope of the curve at that point.

 

[Samar A]

Try: my textbook refers to the slope (of or the tangent) of the voltage curve to be (dV/dt)

It says: (dV/dt) represents the slope of the tangent drawn to the curve.

Slope of the tangent at a point on the function is the derivative of the function at that point. It is a very big topic in calculus, called differential calculus.

Could you be more specific about what you don't understand in that graph?

chh1995, I actually don't study calculus I know only a small amount of information about it. What I want to know is how the value (dV/dt) determines the slope?

 

[Samar A]

Try: My textbook refers to the slope of the voltage versus time curve to be (dV/dt). To find this slope you draw a straight line that is tangential to the voltage curve, and the slope of this straight line is the slope of the curve at that point.

Ok, why the value of (dV/dt) particularly represents the value of the slope?

 

[cnh1995]

chh1995, What I want to know is how the dV/dt determines the slope?

You'll need to study calculus for that..
It is the definition of derivative.
If y=f(x), dy/dx is the slope of the tangent to the curve. Here, voltage V is a function of time t. So, dV/dt represents the slope of the curve (which is same as slope of the tangent to the curve at a point).

As you can see, slope of the voltage curve at its peak point is zero (the tangent is parallel to the time axis). This means, the capacitor current is zero, which is shown in the current waveform.

 

[NascentOxygen]

Ok, why the value of (dV/dt) particularly represents the value of the slope?

Think of it as ∆V/∆t
where ∆V is the small change in V that occurs during a small change in time, ∆t
and you can measure ∆V and ∆t off the graph, choosing ∆t to be any measurable small change in time, i.e., of your own choosing

 

[cnh1995]

You'll need to study calculus for that..
It is the definition of derivative.
If y=f(x), dy/dx is the slope of the tangent to the curve. Here, voltage V is a function of time t. So, dV/dt represents the slope of the curve (which is same as slope of the tangent to the curve at a point).

As you can see, slope of the voltage curve at its peak point is zero (the tangent is parallel to the time axis). This means, the capacitor current is zero, which is shown in the current waveform.

Referring to #7, where Δt is a small (infinitesimal) change in time, the derivative is given by,
dV/dt=lim Δt→0 (ΔV/Δt).

 

[CWatters]

+1

You might also like to think about what happens if you feed a capacitor with a constant current.

 

[Samar A]

+1

You might also like to think about what happens if you feed a capacitor with a constant current.

when feeding the capacitor with a DC source the current of the source flows to charge the capacitor and then it stops when the voltage across the capacitor is equal to the voltage across the terminals of the source. Then, nothing will happen there will be no sinusoidal curve as in the case of the AC source, so I don't know how to think of it as if we fed it with a constant current?!

 

[cnh1995]

when feeding the capacitor with a DC source the current of the source flows to charge the capacitor and then it stops when the voltage across the capacitor is equal to the voltage across the terminals of the source. Then, nothing will happen

Right. But that's the case with "direct" current. Constant current is different. It is a source of constant current (just like a voltage source is a source of constant voltage). I think you haven't studied current sources yet in college.

so I don't know how to think of it as if we fed it with a constant current?!

No. I don't think he is asking you to think about ac in terms of constant current. I believe it is meant to be a small exercise in order to understand how a capacitor responds to different inputs.

 

[Samar A]

Right. But that's the case with "direct" current. Constant current is different. It is a source of constant current (just like a voltage source is a source of constant voltage). I think you haven't studied current sources yet in college.

No. I don't think he is asking you to think about ac in terms of constant current. I believe it is meant to be a small exercise in order to understand how a capacitor responds to different inputs.

Oh, sorry. You are right I didn't study current sources, I am only a high school student. I thought a constant current is a direct current. Anyways, it is okay, I got it and understood the curve of an AC source.

 

[CWatters]

A constant current source delivers a constant current to the load. So given your equation...

I=C(dV/dt)

...if I is constant then dV/dt is constant. The result is that the voltage on the capacitor increases at a constant rate/constant slope. In the real world this can't happen indefinitely as the voltage would get too high, however such a circuit could form the basis of a triangle wave generator.