The Velocity of Block B Relative to A

[kiwifruit]

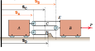
After applying force P, block B accelerates to the right at 3m/s^2
When B has velocity of 2m/s determine:
1.The velocity of B relative to A
2.The acceleration of B relative to A
3.The absolute velocity of point C

The image attached show how this works.
I worked out the total length,L to get

L = 3(Sb - Sa) + (Sd - Sa)
so if you differentiate with respect to t you get

0 = 3 d(Sb - Sa)/dt + d(Sd - Sa)/dt

then I am stuck.

or is the differential equation supposed to be
L = 3(Sb - Sd) + 4(Sd - Sa)
so differentiating would get
0 = 3 d(Sb - Sd)/dt + 4 d(Sd - Sa)/dt

because somehow Va=3/4Vb
if its the second differential equation could someone explain how to get from there to get Va and Vb?

 

[tiny-tim]

hi kiwifruit!

(try using the X₂ icon just above the Reply box )

L = 3(Sb - Sa) + (Sd - Sa)
so if you differentiate with respect to t you get

0 = …

you're making this very complicated …

S_d is constant, so use the equation for L to find S_a as a function of S_b