The voltage of the 2uf capacitor will be the sum of the two source voltages.

[dreamz25]

the topic "capacitors"

Hi everyone!
while i was working out questions on the topic "capacitors", got stuck somewhere...
and my problem is

Suppose the arrangement is like ...

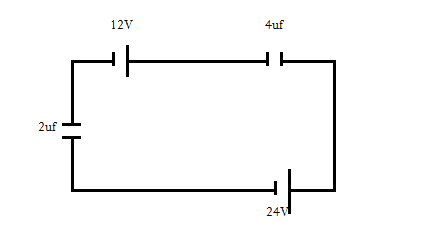
So two questions are points of my confusion...

(1) what will be the direction of flow of current?
(2) and how to find the potential difference between the 2uf capacitor?

My work
I actually tried a lot to work this question out but failed..
main problems were,
* How to put the charges on each capacitor ? ,
* How can there be a potential difference across 2uf capacitor as both of its plates are connected to the -ve plates of the cells.

actually for the first time i have come across the system involving two cells and with such an arrangement.

So please guide me...
I don't want the soln.. but just want to get my concept clear...
simply guide me... how to proceed...?
would be thankful...!

 

[DragonPetter]

Is this question in context of steady state, transient response, or both?

If it is steady state, then question (1) is a trick question (kind of). Question (2) can be found by writing in the - and + terminals of each component at their nodes, with the voltage drop across that component. Use KVL to find the voltage across the unknown nodes. The answer is very simple.

If its transient, then you must use current convention that current flows from + to - voltage and also be aware of initial conditions, which makes me think the question is for steady-state only. Question (2) would be a trick question since there is no resistance, and so the voltage would be changing at an infinite rate.

 

[NascentOxygen]

(1) what will be the direction of flow of current?
(2) and how to find the potential difference between the 2uf capacitor?

The larger voltage source dominates (this is equivalent to saying the polarity of the sum of the voltage sources) and this sets the charging current direction.

There is an inrush of current into the uncharged capacitors until the sum of their voltages = the net source voltage. (In practice, there will also be some resistance in the loop, and this will limit the amplitude of the inrush of current to a value less than infinite.)