B Thermal Insulation Thickness Calculations

[salvatore13]

TL;DR Summary

Derive equation used for insulation calculations.

I found this online calculator for insulation thickness: https://insulation.com.au/calculator/thickness-required/

Can you help me find equation being used for the calculation?

Based on inputs required, my understanding is that it must be heat conduction calculations but also accounting for convection and/or radiation effects on the inside and outside.

 

[BvU]

!

This calculator uses Fouriers law in one diimension. Familiar with that ?

Curiosity can be a reason to reverse-engineer that, but it may be more useful to build up your own calculation. What's your application ?

$\$

 

[Chestermiller]

I don't think that the calculator in your reference includes convective heat transfer resistance inside and outside the insulation.

 

[BvU]

I don't think that the calculator in your reference includes convective heat transfer resistance inside and outside the insulation.

Change input to

and to

indicates it does, or am I mistaken ?

$\$

 

[Chestermiller]

Change input to
View attachment 342317
and to
View attachment 342318
indicates it does, or am I mistaken ?

$\$

Oops. Missed that.

 

[salvatore13]

!

This calculator uses Fouriers law in one diimension. Familiar with that ?

Curiosity can be a reason to reverse-engineer that, but it may be more useful to build up your own calculation. What's your application ?

$\$

I’m calculating insulation thickness for an engine bay with forced air cooling. Known parameters are
- inside air temperature (forced flow)
- outside air temperature (static)
- material properties of the engine bay enclosure and insulation, and finally
- maximum allowed outside surface temperature of the engine bay enclosure

The calculator I’ve given as an example is using all these as an input so this tells me I’m on the right track.

Ideally I’d like to plot the temperature on the outside of the engine bay enclosure vs insulation thickness

I could just use the calculator but I want to understand where the values are coming from just for my own curiosity :)

You mentioned Fouriers law which describes conductivity but this calculator seems to also account for convection. I’m not sure how to tackle that…

 

[BvU]

I want to understand where the values are coming from just for my own curiosity :)

I can appreciate that !

Basically you have heat transfer $\dot Q$ over a series of resistances going from $T_{hot}$ to $T_{cold}$.

As with conductance, there is a relationship $\dot Q = h A \Delta T$ where all the knowledge is in the convection heat transfer coefficient $h$ ( W/(m²$\cdot$K) ).
$\Delta T$ is the temperature difference between surface and bulk.

Ominously, my thermodynamics book (Cengel) says $h$ is an experimentally determined parameter whose value depends on all the variables that ... etc. Typical is 25-250 W/(m²$\cdot$K for forced convection of gases. Hmm...

(your calculator uses $h = 22$ it seems: 146 degrees with 'Inside surface temp equals operating temp' gives the same 22.48 mm).

$\$

 

[salvatore13]

I can appreciate that !

Basically you have heat transfer $\dot Q$ over a series of resistances going from $T_{hot}$ to $T_{cold}$.

As with conductance, there is a relationship $\dot Q = h A \Delta T$ where all the knowledge is in the convection heat transfer coefficient $h$ ( W/(m²$\cdot$K) ).
$\Delta T$ is the temperature difference between surface and bulk.

Ominously, my thermodynamics book (Cengel) says $h$ is an experimentally determined parameter whose value depends on all the variables that ... etc. Typical is 25-250 W/(m²$\cdot$K for forced convection of gases. Hmm...

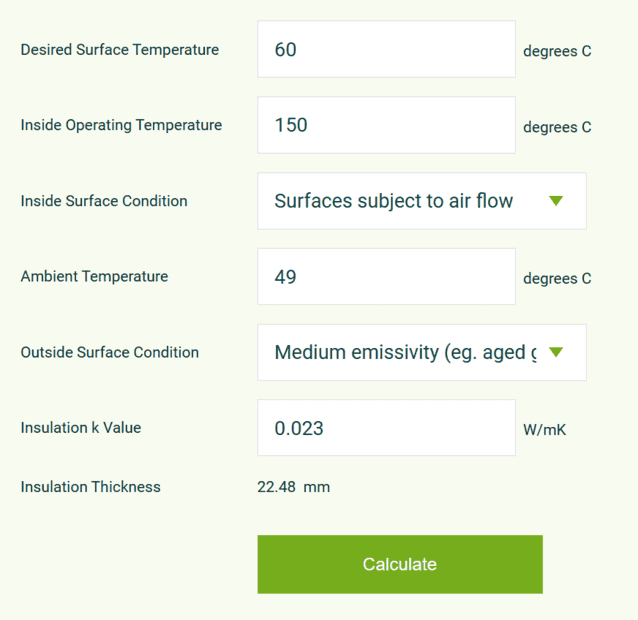
(your calculator uses $h = 22$ it seems: 146 degrees with 'Inside surface temp equals operating temp' gives the same 22.48 mm).

$\$

Thanks for the tip - I've tried to solve the problem and my equations give me somewhat sensible results but they don't match the result from the calculator. I'll try to walk you through it briefly.

The diagram for the problem:

For thermal equilibrium, I'm assuming that heat flux in and outside the panel must be equal so that temperatures remain constant.
$\dot Q_1 = \dot Q_2 = \dot Q_3$ because $T_1,T_2, T_{outside}, T_{inside} = constant$

For the worst-case scenario, $\dot Q_1$ can be omitted and simply
$T_1 = T_{inside}$

For Conduction through the insulation ($\dot Q_2$):
$\frac {\dot Q_2}{A} = \frac {T_1-T_2}{\frac {t_{ins}}{k_{ins}}}$
I'm ignoring the aluminium panel as it has a negligible thermal resistance.

For Convection between insulation and outside ambient air ($\dot Q_3$):
$\frac {\dot Q_3}{A} = h_3(T_2-T_{outside})$

So since:
$\dot Q_2 = \dot Q_3$

Then:
$\frac {T_1-T_2}{\frac {t_{ins}}{k_{ins}}} = h_3(T_2-T_{outside})$

And from that I come up with this solution for thickness:
$t_{ins} = \frac {k_{ins}(T_1-T_2)}{h_3(T_2-T_{out})}$

But when I plug in the same input from the calculator and h = 22, the result is thickness = 8.5mm instead 22.48 as it should be.

Any advice on what I'm doing wrong? :)

 

[Chestermiller]

Let $T_3$ be the temperature between the aluminum and the insulation. Then, $$T_{outside}-T_1=\frac{q}{h_{outside}}$$
$$T_1-T_3=q\frac{b_{insulation}}{k_{insulation}}$$$$T_3-T_2=q\frac{b_{aluminum}}{k_{aluminum}}$$$$T_2-T_{inside}=\frac{q}{h_{inside}}$$. Add these equations together to eliminate T1, T2, and T3