Thevenin Equivalent : Wrong value for Rth

[AfterSunShine]

Homework Statement

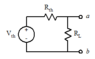
The problem ask for Thevenin Equivalent for the circuit attached.

Homework Equations

Vth = Vab
Rth = Req
Rth = Vth / Isc
Rth = 1 / It

The Attempt at a Solution

Already calculated Vth = 166.67 V. I've no problem with that. Already confirmed by textbook answer.
However, my issue is with Rth,
As per book there 3 methods to calculate Rth

1st Method : Kill independent sources and Rth = Req as seen by terminals. (Provided all sources in the circuit are independent).
2nd Method : Make a wire (short circuit) between a & b going from a to b. Calculate current of this wire (Isc), Req = Vth / Isc
3rd Method : Kill independent source, Put test voltage source with value 1 V, Put test current (It) going from - to + , calculate current, Rth = 1 / It

For the attached circuit, 1st method cannot be used as there is dependent source in the circuit.
I used third method and got Rth = 10 ohm, which is the correct answer.
My issue with the 2nd method !
If i used the second method and make short circuit between a & b, 10 ohm will be removed as it is parallel with short circuit. Then i calculate Isc and it is zero ! i used different methods (kcl kvl, mesh) still zero!
which will make Rth = 166.67 / 0 = infinity! which wrong for sure. Answer should be Rth = 10 ohm

My questions are :
(1) Did i summarize the methods correctly?
(2) Why is Isc = 0 when I use the second method?

Thanks in advance.

 

[Charles Link]

Method 2 works. $I_{sc} \neq 0$. Ignore the dependent current source which will just feed into the short circuit for the time being. You have $6 \, \Omega$ in parallel with $2 \, \Omega$. That makes $1.5 \, \Omega$ in series with $3 \, \Omega$. That means $I_{total}=50/(4.5)$. Compute how this distributes itself. Then compute the dependent current as well. I do get $10 \, \Omega$ for $R_{th}$ by the short circuit current method. $\\$ One question: Did you conclude $I_1= (\frac{50}{4.5})( \frac{1}{4})( \frac{6}{2})$ cancels $I_2= (\frac{50}{4.5})( \frac{3}{4})$ ? The currents add. They don't cancel.

 

[AfterSunShine]

"Ignore the dependent current source which will just feed into the short circuit for the time being."
Am not following you !
So whenever I have current source parallel with short circuit, I just kill the source i.e. making it open circuit?
Explain pelase.

Edit:
Let me generalize my question : Current source is parallel with short circuit, can i just deactivate the source and deal normally with whatever circuit am dealing with?

 

[Charles Link]

"Ignore the dependent current source which will just feed into the short circuit for the time being."
Am not following you !
So whenever I have current source parallel with short circuit, I just kill the source i.e. making it open circuit?
Explain pelase.

The current source there is going to superimpose on whatever occurs if you considerthe current sourcet momentarily as an open circuit that is shut off. It is going to feed into a short circuit in this problem where you are computing the short circuit current. It thereby will not affect any current that is already in that short-circuit=it simply will get added to it. If you do the arithmetic I included there, you just add those two currents to get the short circuit current for this problem.$\\$ 3/4 of the current from the 50 volt source goes through the 2 ohm resistor (call it $I_2$), and 1/4 of it through the 6 ohm resistor. Added to the short circuit current across "ab" from the 2 ohm resistor path is the current ($I_1$) from the current source. $\\$ For this problem, those currents are equal and add to give $I_{sc}=150/9$.

 

[AfterSunShine]

Thanks for you reply,
I solved it using two different ways.

(1) First solution :
Taking 2 parallel with 6 & redraw circuit, solve it as shown in attach file. I redraw the circuit as our instructor said : " When taking two resistors in parallel, replace one of the resistors by the equivalent R and remove the other resistor".
As per attached file ,Getting Isc = 8.33 A, Rth = 20 ohm which wrong for sure.
What is my mistake ?

(2) Second solution :
Using mesh method, I got the right answer !
Isc = 16.67 , Rth = Vth / Isc = 166.67/16.67 = 10 ohm,

 

[Charles Link]

You must include the dependent current source which supplies the other 8.33 amps. That is what is wrong with your first solution using method 2. $\\$ Edit: I see what you did=you computed the dependent current, but you need to add the current that goes through the 2 ohm resistor. That current in this problem is the same value as the dependent current, and it adds to it. $\\$ Perhaps you are making the mistake that the dependent current source is a short circuit path for this other 8.33 amps. That is not the case. If you compute it, there is 8.33 amps going through the 2 ohm resistor. Where does it go? It should wind up going through the short circuit that you make across "ab".

 

[AfterSunShine]

Finally i got it!
Oh god the headache gone.
Thank you sir.

 

[gneill]

Finally i got it!
Oh god the headache gone.
Thank you sir.

If I might offer up another approach that I thought of back in my school days (when dinosaurs ruled the Earth) and served me quite well for these sorts of circuit problems. I am sure is not unique since there are far more clever people than myself publishing circuit analysis methods, but I offer it up such as it is.

I considered the situation where a Thevenin source was driving a load resistance and how it was basically a voltage source with a source resistance and a load resistance in a voltage divider configuration:

$V_{ab} = V_{th} \frac{R_L}{R_L + R_{th}}$

So I thought to myself that if a circuit analysis could be made to determine the voltage across some arbitrary load resistance, that analysis should result in a formula that could be put into the form of a voltage divider equation from which you could pick out the Thevenin voltage and Thevenin resistance. Two birds with one stone, as it were.

Your circuit is one such circuit.

Let's add to your circuit a load resistance and choose the bottom rail as the reference node, then label the two essential nodes $V_1$ and $V_2$, with $V_2$ being recognized as the output voltage $V_{ab}$.

Employing nodal analysis, we can write:

For node $(V_1)$:

$\frac{V_1-50}{3} + \frac{V_1}{6} + \frac{V_1 - V_2}{2} = 0$

so that:

$V_1 = \frac{50}{3} + \frac{1}{2} V_2$

For node $V_2$:

$\frac{V_2 - V_1}{2} - \frac{1}{2} V_1 + \frac{V_2}{10} + \frac{V_2}{R_L} = 0~~~~~~$ as v_x = V₁ given the chosen reference node

Collecting terms:

$\left( \frac{3}{5} + \frac{1}{R_L} \right) V_2 - V_1 = 0$

Substituting for $V_1$ from before,

$\left(\frac{3}{5} + \frac{1}{R_L} \right) V_2 - \left( \frac{50}{3} + \frac{1}{2} V_2 \right) = 0$

Solve for $V_2$:

$V_2 = \frac{500}{3(R_L + 10)}R_L$

Adjusting the result to resemble a voltage divider equation:

$V_2 = \frac{500}{3} \frac{R_L}{R_L + 10}$

Comparing the result with voltage divider equation where a Thevenin source drives a load, we can easily pick out the Thevenin voltage and resistance:

$V_{th} = \frac{500}{3} V$
$R_{th} = 10 \Omega$

I hope that this contribution might prove helpful in your future studies.