- #1
Martel
- 3
- 1
- Homework Statement
- Statement provided as an image
- Relevant Equations
- Equations provided at the end of the post (latex and SageMath/Python)
I have a problem which consist in 1 bit RAM made of 3 MOSFETs. One of the questions is to calculate the maximum voltage that the memory element can receive. I have obtained the result by inspection (it is 4 Volts) but I'm unable to reach the same by applying the Thevenin Theorem.
My understanding is: I have a circuit made of several resistors and one capacitor (which is the memory element). If the circuit is reduced to a $ (V_{TH}, R_{TH}) $ Thevening Equivalent, and given that the capacitor behaves like an open circuit for long periods of time (it's fully charged), I can assume that the maximum voltage the capacitor might have is $ V_{TH} $. The problem is that the $ V_{TH} $ I find has nothing to do with the expected result (4 Volts).
**I want to know what I'm doing wrong and how to solve this problem by applying the Thevenin theorem.**
The exercise, along with all my schemas and equations, are below:
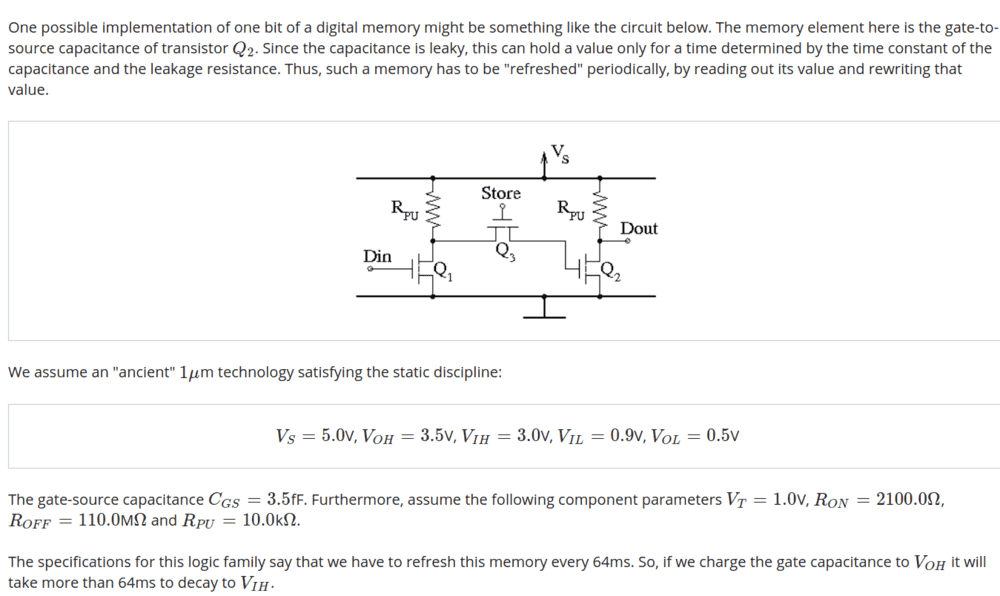
In a previous question I have calculated the parasitic resistance and it is $ R_{PA} = 185.347405560882 $ TeraOhms.
The question I actually need to answer is:
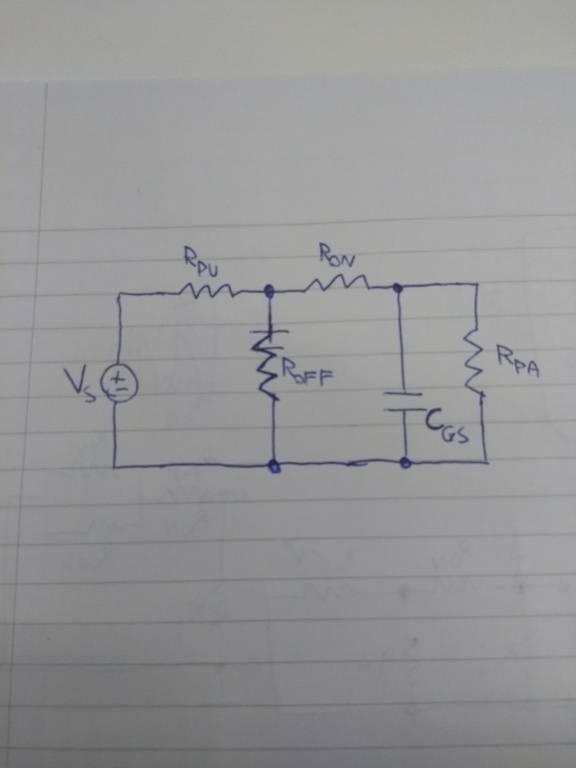
Now, my 'Tehevening Equivalent' attempt to find the voltage in Q2 is below:
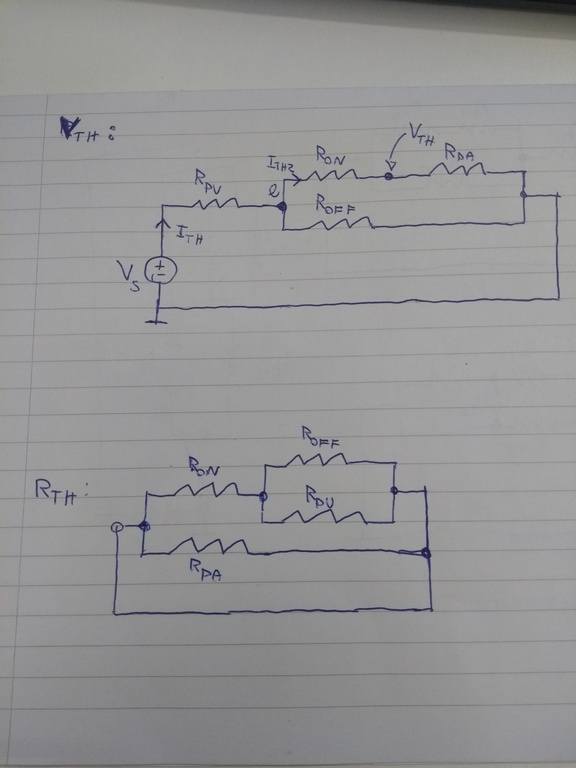
$$
parallel(R_{1}, R_{2}) = \frac{1.00000000000000}{\frac{1.00000000000000}{R_{1}} + \frac{1.00000000000000}{R_{2}}}
\\
R_{\mathit{TH}} = {\rm parallel}\left(R_{\mathit{PA}}, R_{\mathit{ON}} + {\rm parallel}\left(R_{\mathit{OFF}}, R_{\mathit{PU}}\right)\right)
\\
I_{\mathit{TH}} = \frac{V_{S}}{R_{\mathit{PU}} + {\rm parallel}\left(R_{\mathit{OFF}}, R_{\mathit{ON}} + R_{\mathit{PA}}\right)}
\\
e = -I_{\mathit{TH}} R_{\mathit{PU}} + V_{S}
\\
\mathit{ITH}_{2} = \frac{e}{R_{\mathit{ON}} + R_{\mathit{PA}}}
\\
V_{\mathit{TH}} = -\mathit{ITH}_{2} R_{\mathit{ON}} + e
$$
Or in `SageMath`/`Python`:
[CODE lang="python" title="Equations in SageMath/Python"]V_S = 5.
R_ON = 2100
R_OFF = 110e6
R_PU = 10e3
R_PA = 185.347405560882e12 # Parasitic resistance
parallel(R1, R2) = 1./(1./R1 + 1./R2)
R_TH = parallel(R_PA, R_ON + parallel(R_OFF, R_PU))
I_TH = V_S / (R_PU + parallel(R_OFF, R_ON + R_PA))
e = V_S - I_TH * R_PU
I_TH2 = e / (R_ON + R_PA)
V_TH = e - I_TH2*R_ON[/CODE]
The final result (`V_TH`) I get is `4.99954549553765` Volts, and it should be 4 Volts.
My understanding is: I have a circuit made of several resistors and one capacitor (which is the memory element). If the circuit is reduced to a $ (V_{TH}, R_{TH}) $ Thevening Equivalent, and given that the capacitor behaves like an open circuit for long periods of time (it's fully charged), I can assume that the maximum voltage the capacitor might have is $ V_{TH} $. The problem is that the $ V_{TH} $ I find has nothing to do with the expected result (4 Volts).
**I want to know what I'm doing wrong and how to solve this problem by applying the Thevenin theorem.**
The exercise, along with all my schemas and equations, are below:
In a previous question I have calculated the parasitic resistance and it is $ R_{PA} = 185.347405560882 $ TeraOhms.
The question I actually need to answer is:
Now, my 'Tehevening Equivalent' attempt to find the voltage in Q2 is below:
$$
parallel(R_{1}, R_{2}) = \frac{1.00000000000000}{\frac{1.00000000000000}{R_{1}} + \frac{1.00000000000000}{R_{2}}}
\\
R_{\mathit{TH}} = {\rm parallel}\left(R_{\mathit{PA}}, R_{\mathit{ON}} + {\rm parallel}\left(R_{\mathit{OFF}}, R_{\mathit{PU}}\right)\right)
\\
I_{\mathit{TH}} = \frac{V_{S}}{R_{\mathit{PU}} + {\rm parallel}\left(R_{\mathit{OFF}}, R_{\mathit{ON}} + R_{\mathit{PA}}\right)}
\\
e = -I_{\mathit{TH}} R_{\mathit{PU}} + V_{S}
\\
\mathit{ITH}_{2} = \frac{e}{R_{\mathit{ON}} + R_{\mathit{PA}}}
\\
V_{\mathit{TH}} = -\mathit{ITH}_{2} R_{\mathit{ON}} + e
$$
Or in `SageMath`/`Python`:
[CODE lang="python" title="Equations in SageMath/Python"]V_S = 5.
R_ON = 2100
R_OFF = 110e6
R_PU = 10e3
R_PA = 185.347405560882e12 # Parasitic resistance
parallel(R1, R2) = 1./(1./R1 + 1./R2)
R_TH = parallel(R_PA, R_ON + parallel(R_OFF, R_PU))
I_TH = V_S / (R_PU + parallel(R_OFF, R_ON + R_PA))
e = V_S - I_TH * R_PU
I_TH2 = e / (R_ON + R_PA)
V_TH = e - I_TH2*R_ON[/CODE]
The final result (`V_TH`) I get is `4.99954549553765` Volts, and it should be 4 Volts.