You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Thin walled Beams Question
- Thread starter tigerstyle
- Start date
-
- Tags
- Beams
AI Thread Summary
The discussion focuses on calculating the centroid and second moment of area for a hollow thin-walled trapezoidal beam. Participants suggest creating a table to organize the areas and distances of centroids for each member, emphasizing the importance of accurately determining distances from a reference axis. Confusion arises regarding the angles of certain sides and the application of the sine rule to find vertical distances. The conversation also addresses calculating shear flow and shear force, with references to relevant formulas and the need for understanding the second moment of area for inclined surfaces. Overall, the thread provides guidance on approaching the problem methodically and using geometric principles effectively.
Physics news on Phys.org
pongo38
- 739
- 27
You haven't shown your attempt at a solution. In this sort of question I find it helpful to draw up a table showing ( for the four members) area, distance of centroid from a reference axis. moment of area, etc. Can you try something like that?
tigerstyle
- 13
- 0
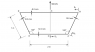
in the question it says find the centroid and second moment of area about the horizontal axis at the centroid. i am confused in the distance of centroid from reference axis for each rectangle, when doing the table. can you please guide me how to do this question. i am using the centroid formula : c=first moment of area/ total area of the section
rock.freak667
Homework Helper
- 6,221
- 31
The centroid of a rectangle would be at its geometric centre. So if the length is a, the width is b, the centroid would be at a length of a/2 and a width of b/2.
Draw the centroids of each member in separate diagrams. If your reference axis is side BD, then where you drew your centroids, calculate the distance of that centroid to the axis.
Take y as vertical and x as horizontal.
For the rectangle BD, the 'y' distance from the reference axis along BD is 4 mm (8/2)
Do the same for each member.
Draw the centroids of each member in separate diagrams. If your reference axis is side BD, then where you drew your centroids, calculate the distance of that centroid to the axis.
Take y as vertical and x as horizontal.
For the rectangle BD, the 'y' distance from the reference axis along BD is 4 mm (8/2)
Do the same for each member.
tigerstyle
- 13
- 0
but what about the side DE and AB because they are at an angle 120 degree. or do i use sin rule at the centroid of DE to find the height?
Thanks
Thanks
tigerstyle
- 13
- 0
i have tried doing a solution and the centroid in y-axis is coming as 0.444m. i don't know if that is right or wrong. can you please check it.
thanks
thanks
tigerstyle
- 13
- 0
and for the second moment of area i have got 15x10^-3 m^4. can anyone check if that's right please
thanks
thanks
rock.freak667
Homework Helper
- 6,221
- 31
tigerstyle said:but what about the side DE and AB because they are at an angle 120 degree. or do i use sin rule at the centroid of DE to find the height?
Thanks
What distance did you use for side AB and DE?
tigerstyle
- 13
- 0
rock.freak667 said:What distance did you use for side AB and DE?
I used sin rule to calculate it and it came as 0.866m.
rock.freak667
Homework Helper
- 6,221
- 31
tigerstyle said:I used sin rule to calculate it and it came as 0.866m.
0.866 m would be the height of triangle formed, you didn't account for the centroid being halfway down the rectangle.
tigerstyle
- 13
- 0
rock.freak667 said:0.866 m would be the height of triangle formed, you didn't account for the centroid being halfway down the rectangle.
what i did for rectangle DE and AB: the midpoint will be 0.5m. and then drew a triangle and used sin rule to find the height of centroid vertically. is that right?
tigerstyle
- 13
- 0
i mean to find the y distance from the base to the midpoint of the rectangle AB and DE
rock.freak667
Homework Helper
- 6,221
- 31
tigerstyle said:what i did for rectangle DE and AB: the midpoint will be 0.5m. and then drew a triangle and used sin rule to find the height of centroid vertically. is that right?
Yes that is right. But when you consider where the centroid is, the hypotenuse is 0.5 mm, so the vertical distance is 0.5sin(60) mm.
tigerstyle
- 13
- 0
I have got the centroid and the second moment for this problem. and have found the shear flow in the walls. now the question is asking me to evaluate the shear force in the walls. i don't know what that means. can you help please
thanks
thanks
tigerstyle
- 13
- 0
and sketch the shear flow in the cross section. i am really struggling on this as i don't know how to do it. your help will be much appreciated.
thanks
thanks
rock.freak667
Homework Helper
- 6,221
- 31
tigerstyle said:I have got the centroid and the second moment for this problem. and have found the shear flow in the walls. now the question is asking me to evaluate the shear force in the walls. i don't know what that means. can you help please
thanks
How did you calculate the shear flow? Shear flow is related to the shear force, first moment of area and second moment of area.
tigerstyle
- 13
- 0
i used da formula q=q0 - (Vy/Ixx) Integral t*y*ds and calculated it for qOA, qAB and qBC. qBC = 0 as it lies on the axis of symmetry.
tigerstyle
- 13
- 0
rock.freak667 said:How did you calculate the shear flow? Shear flow is related to the shear force, first moment of area and second moment of area.
i used da formula q=q0 - (Vy/Ixx) Integral t*y*ds and calculated it for qOA, qAB and qBC. qBC = 0 as it lies on the axis of symmetry.
tigerstyle
- 13
- 0
where Vy=Vertical shear force given in the diagram and Ixx =second moment of area calculated as 101.25 x 10^8 mm4, t=thickness and y is the distance to the centroid
rushit_31
- 3
- 0
how did u calculate the second moment of area??
Can you please help me?
Can you please help me?
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,815
- 1,673
rushit_31 said:how did u calculate the second moment of area??
Can you please help me?
What have you tried? Do you understand the calculation?
rushit_31
- 3
- 0
I am not understanding how to calculate the second moment of area for the inclined surfaces??
is it calculated using bh3^3/12 or by using integration...
is it calculated using bh3^3/12 or by using integration...
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,815
- 1,673
You can calculate the moment of inertia of the inclined surface as if it were not inclined, and then transform the values using a process similar to the parallel axis theorem.
The following article describes the process (pages A-16 and A-17):
http://mbarkey.eng.ua.edu/courses/AEM250/CRAIG_007-021_APPC.pdf
The following article describes the process (pages A-16 and A-17):
http://mbarkey.eng.ua.edu/courses/AEM250/CRAIG_007-021_APPC.pdf
rushit_31
- 3
- 0
how did u get the second moment of inertia for the DE and AB??
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,815
- 1,673
Did you read the attachment in Post #23? It contains the formulas you need to do the calculation. You take the length and thickness of the side plates and calculate Ix and Iy as if the plates were standing vertical. Then, using the angles from the cross-section diagram, you transform Ix and Iy for the sides into Ix' and Iy' to be used in the cross-section inertia calculation.
Similar threads
Engineering
Deflection and Slope of a Simply Supported Beam
- Replies
- 8
- Views
- 2K
- Replies
- 9
- Views
- 4K
- Replies
- 2
- Views
- 2K
- Replies
- 45
- Views
- 7K
- Replies
- 8
- Views
- 2K
- Replies
- 10
- Views
- 4K
- Replies
- 1
- Views
- 3K
- Replies
- 2
- Views
- 3K
- Replies
- 2
- Views
- 2K
- Replies
- 1
- Views
- 1K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Spiral scissor lift statics
- Started by carlcla
- Replies: 4
- Engineering and Comp Sci Homework Help
-
Engineering Diff gain of a push pull degenerated differential pair
- Started by arhzz
- Replies: 6
- Engineering and Comp Sci Homework Help
-
Engineering AGMA pitting resistance factor of safety (SH)
- Started by ironfalls18
- Replies: 2
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math