SUMMARY
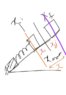
This discussion centers on calculating the work done by a spring on an inclined plane involving three blocks. The Work Energy Theorem is applied, with specific focus on the tension in the spring when block A loses contact. Participants emphasize the importance of considering spring potential energy (PE), gravitational potential energy (GPE), and kinetic energy (KE) in the analysis. Key equations discussed include W_gravity on B=1*x*g*sin(37) and the relationship between variables xi, xj, and x.
PREREQUISITES
- Understanding of the Work Energy Theorem
- Knowledge of spring potential energy (PE) and gravitational potential energy (GPE)
- Familiarity with basic mechanics involving inclined planes
- Ability to manipulate algebraic equations for solving physics problems
NEXT STEPS
- Study the application of the Work Energy Theorem in various mechanics problems
- Learn about the dynamics of springs and Hooke's Law
- Explore the relationship between kinetic energy and potential energy in mechanical systems
- Investigate the effects of inclined planes on force and motion
USEFUL FOR
Students studying physics, particularly those focusing on mechanics, as well as educators looking for examples of applying the Work Energy Theorem in problem-solving scenarios.