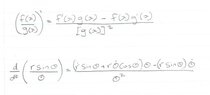Time derivative using the quotient rule

In summary, the quotient rule is a formula used in calculus to find the derivative of a function that is written as a ratio of two other functions. It is important because it simplifies the process of finding derivatives and is useful in real-world applications. The steps for using the quotient rule include identifying the functions, taking the derivative of each separately, plugging them into the formula, and simplifying the resulting expression. It can only be applied to functions in the form of a ratio and common mistakes to watch out for include forgetting the negative sign and not simplifying the expression enough.
  • #1
Mishal0488
18
1
Hi Guys

Sorry for the rudimentary post. I am busy with a numerical solution to a mechanics problem, and the results are just not as expected. I am re-checking the mathematics to ensure that all is in order in doing so I am second guessing a few things

Referring to the attached scan, is the quotient rule used correctly when taking the time derivative of the function? Note that both "r" and "theta" are time dependent.

Thanks in advance
 

Attachments

  • Capture.JPG
    Capture.JPG
    10.4 KB · Views: 104
Physics news on Phys.org
  • #2
Looks right.
 

Similar threads

I Time Derivatives: Hi Guys, Am I on the Right Track?
Replies
3
Views
697
I Question about the quotient rule of derivatives
Replies
12
Views
4K
I Why is the derivative defined as the limit of the quotient?
Replies
13
Views
2K
I Treating the Derivative like a Quotient
Replies
15
Views
2K
I Using reference frames for derivation of Lagrangian
Replies
25
Views
2K
Limit question to be done without using derivatives
Replies
25
Views
1K
A Question on Zeno time derivation
Replies
4
Views
1K
B Proof of quotient rule using Leibniz differentials
Replies
9
Views
5K
Sinking Object Motion Equations
Replies
6
Views
2K
Derivative of a fractional function without quotient rule
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top