Time Dilation and different clock types

[MidiMagic]

Here is a thought experiment to show that it is relativity and the properties of spacetime, not something affecting the mechanism of the clock.

Case 1 is the case the original post posited: One clock is put into a vehicle moving relative to you at a constant velocity. You and an identical clock are left behind. Then you observe the clocks from your frame of reference.

Case 2 is a case that should be equivalent in relativity. You get into a vehicle moving at a constant velocity, taking one clock, and leaving an identical clock behind. Then you observe the clocks from your frame of reference.

Relativity says that both observations should produce the same result. You should observe the clock in the other frame of reference running slower than the clock you have with you runs.

 

[Raymond Potvin]

OK, then the old Twin's paradox is solved: reunited in the middle of the two observers, the two clocks should show the same time, which would contradict the light clock predictions. Here is some thinking I made about that light clock mind experiment, and it seems to contradict relativity, so you tell me where I am wrong.

A light clock runs slow because the light path lengthens and the clock takes longer to tick over.

Hi guys, hi DAC,

Elapsed time is not measured with light paths, but with frequencies, thus with light waves if the clock is a light clock. The light clock mind experiment shows a longer path for the light ray, but it doesn't show how this longer distance would be accounted for by the clock. If we replace the two mirrors by a light source and an observer, there would be no way for the observer to measure that distance, because even if, to travel in the direction of the future position of the observer, the ray was emitted at an angle to the direction of motion, thus producing doppler effect at the source, this effect would be nullified at the observer because he would be meeting the same ray at the same angle and at the same speed but in the opposite direction. Moreover, he would have no way to measure the real direction of the ray either because aberration at the observer would indicate that the source was not in motion. Here is a drawing I made about that:

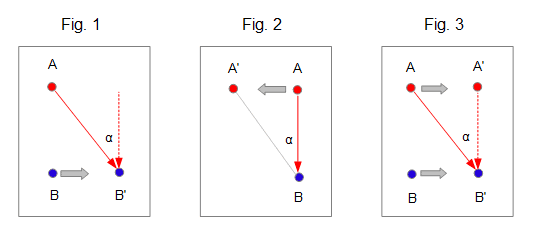
Fig. 1 and 2 show how aberration and doppler effect occur for two bodies moving in different reference frames. Fig. 3 shows how aberration and doppler effect could actually be occurring at the source but would later be nullified at the observer, thus would always be unobservable, for bodies moving in the same reference frame.

At fig. 1, the observer is considered moving while the source is at rest. While the observer at B travels to B', light travels from A to B', so for the observer at B', the light ray suffers the aberration angle α and has the apparent direction of the dotted red arrow, but it also suffers doppler effect because the observer is moving at an angle to the incoming ray.

At fig. 2, the source is considered moving while the observer is at rest. While the source at A travels to A', light travels from A to B, so for the observer at B, the light ray does not suffer aberration but has the same apparent direction as in fig. 1. For us, it makes the same angle α with A'B, and it does not suffer doppler effect because the ray was emitted at a normal to the motion of the source, but it suffers relativistic doppler effect, which gives exactly the same number as in fig. 1 where the observer's speed was producing doppler effect while moving at an angle to the ray.

At fig. 3, both source and observer are considered moving at the same speed and in the same direction, so the only difference with fig. 1 is that the source is also traveling. For the observer at B', the light ray still has the same apparent direction as in fig. 1 since it suffers the same aberration angle, but this time, its direction points to the actual position of the light source because it has traveled the same distance as the observer, there is no measurable doppler effect because the one produced at the source nullifies the one produced at the observer, and there is no measurable relativistic doppler effect either because the two sources travel at the same speed. Of course, it would give the same result if the observer was at A and the source at B.

To me, fig. 3 means that if the source was a laser beam aimed perpendicularly to its motion, this beam would never hit the observer, which seems to contradict the reference frame principle. Does it?

 

[MidiMagic]

"OK, then the old Twin's paradox is solved: reunited in the middle of the two observers, the two clocks should show the same time, which would contradict the light clock predictions."

Not so fast.

1. When something is accelerated from one frame of reference to another, clocks that were in synchronization before the acceleration will not be in sync after the acceleration takes place from the point of view of either frame of reference.

2. To bring the two clocks back together, at least two more accelerations must take place. These further unsynchronize the two clocks.

One thing to think about in the light clock and light propagation drawings: Try making the drawings again as though you are sitting in the other frame of reference.

 

[Raymond Potvin]

To bring the two clocks back together, at least two more accelerations must take place. These further unsynchronize the two clocks.

If both accelerations would be the same, the clocks should stay synchronized.

One thing to think about in the light clock and light propagation drawings: Try making the drawings again as though you are sitting in the other frame of reference.

Drawing 1 and 2 show the two viewpoints, and drawing three shows both at a time, because we can interchange observer and source.

 

[Janus]

If both accelerations would be the same, the clocks should stay synchronized.

It is not just the magnitude of the acceleration that counts, it is also the distance between the clocks and there direction with respect to each other relative to the acceleration that factors in.
If if both clocks start at the same point and one clock then undergoes a short intense acceleration, due to the fact that there is no to little separation distance between the two clocks, the acceleration causes only a small additional difference in the clock readings. However, when that clock reaches a point some distance from the other clock and then decelerates to a stop and then accelerates back to the other clock, the large separation distance between the clocks will cause the other clock to run fast from his perspective. If he then decelerates upon his return, the small distance between the two clocks again results in only a small difference.

From the accelerating clock's view, the acceleration he undergoes when the clocks are separated at the turn around has a much more profound effect on the relative clock readings than the acceleration he undergoes when the clocks are adjacent or very near each other.

 

[Raymond Potvin]

Hi Janus,

If both clocks were departing directly from one another prior to getting back together, then their first deceleration could be the same, their acceleration towards one another also, and their last deceleration also, so it should produce no difference in their timing, what would sort of solve the paradox. But my questioning was about the light clock. What do you think of that reasoning?

 

[Dale]

@Raymond Potvin please do not hijack other people's threads. This would be far more appropriate as its own thread.

In a light clock the time is not measured using the frequency of the light, the Doppler shift is 0 and the actual frequency is not relevant. The time is measured by measuring the "echo time" from a target at a known range.