name
- 9
- 1
- Homework Statement
- Calculate the time it takes for the light to travel a straight line distance d1 in a bus moving at a constant velocity V as observed by an external observer.
- Relevant Equations
- N/A derived below.
So I drew the problem and tried to derive t1 for an external observer by making the following assumptions.
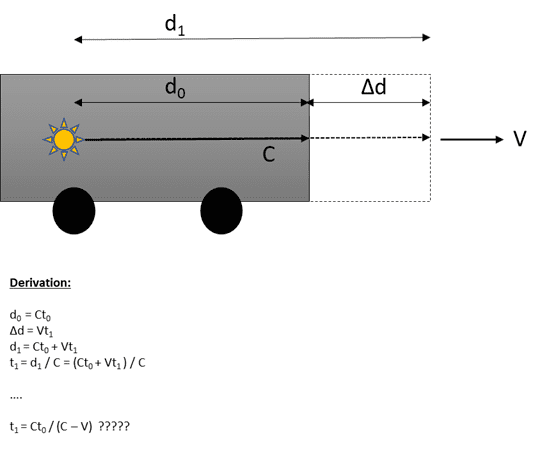
I know this is incorrect but I don't see where the error is?
Thank You
- Inside observer sees light travel a distance of d0 meters in t0 seconds at a speed of c m/s.
- Bus moved Δd meters in t1 seconds at V m/s.
- Outside observer sees light travel a distance of d1 meters in t1 seconds at a speed of c m/s.
I know this is incorrect but I don't see where the error is?
Thank You
Last edited by a moderator:
