Porter Tawa
- 2
- 0
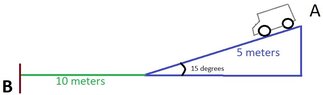
A 2000 kg truck is resting at the top of a parking lot ramp which is at a 15 degree slope. It is then shifted into Neutral and starts moving.
How long does it take the truck to get from A to B in seconds?
There is a 15 degree slope on the ramp.
uk is 0.08
Assume there is no air resistance.
How long does it take the truck to get from A to B in seconds?
There is a 15 degree slope on the ramp.
uk is 0.08
Assume there is no air resistance.