Time period of an oscillating body

[s0ft]

In the above figure, what would be the time period of the body(in red) under gravity, neglecting any non-conservative forces?
And what do call this type of situation? A gravity well or sth?

 

[Redbelly98]

The question cannot be answered unless you provide a distance scale. Also, what is that shape supposed to be? Is it parabolic, or something else?

p.s welcome to Physics Forums.

 

[s0ft]

The shape can be taken to be parabolic, if it simplifies things. And if this is what you wanted me to clarify, the value of acceleration due to gravity can be taken to be a constant.
And I'm most thankful for the welcome.

 

[Vanadium 50]

You still need a length scale. Does a shallow parabola have the same period as a deep one?

 

[s0ft]

You may take any case as long as it doesn't look a wholly different problem. And you're most welcome to give any well put example for the problem of this sort, if it is possible. I just want to get a general idea about this.

 

[Vanadium 50]

This is "how long is a piece of string". The period will be proportional to sqrt(g/L), where L is some characteristic length scale in the problem. If you don't give us L, we can't give you t.

 

[s0ft]

I don't mean to get a numerical value. Just take some variables and show me the way it's done. That's all. Or is there something else to it that I don't understand?
I just want to know how you get to the sqrt(g/L) part.

 

[Redbelly98]

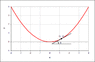
Just take some variables and show me the way it's done.

Okay, I think we can work something out here. Hope you're familiar with calculus

Let L be the length defined by

Height above valley bottom = Horizontal distance from valley bottom​

I.e., to find L, draw a 45 degree line from the red dot. The line will intersect the curve at the height L.

The level or height of the ground, above the valley bottom, is then given by
\begin{align}<br /> &amp; y/L = (x/L)^2 \\<br /> \text{or} &amp;\\<br /> &amp; y = x^2 / L<br /> \end{align}<br />
(Check for yourself that this equation has the two desired properties: (1) it is a parabola, and (2) y=L when x=L)

Now apply Newton's 2nd Law for the horizontal (x-direction) motion:

[Edit: added cosθ term below]
\begin{align}<br /> ma &amp; =F \\<br /> \\<br /> m \frac{d^2x}{dt^2} &amp;= -mg \sin \theta \cos \theta, \\<br /> \end{align}
where θ is the angle of the slope.

If we restrict the motion to small-amplitude oscillations (i.e. x is much smaller than L), then we can make the approximation
<br /> \sin \theta \cos \theta \approx \theta \approx \tan \theta = \frac{dy}{dx} = \frac{2x}{L}<br />[Edit: added cosθ term above]

Substituting this for sinθ in the earlier equation, we get

\begin{align}<br /> m \frac{d^2x}{dt^2} &amp;= -mg \frac{2x}{L} \\<br /> \\<br /> \frac{d^2x}{dt^2} &amp; = -\frac{2g}{L}x \\<br /> \end{align}

This is a well-known differential equation, with the particle oscillating sinusoidally at angular frequency
\omega = \sqrt{\frac{2g}{L}} \text{ in radians/second}
So the period of oscillation would be
T = \frac{2 \pi}{\omega}<br /> = 2 \pi \sqrt{\frac{L}{2g}} <br />
Using g≈10 m/s², you can calculate the period for, say L=0.3 meter -- or about 1 foot, the size of a hole you might dig in the ground with a shovel.

 

[s0ft]

Thank you very much!
But I didn't quite get the y and x, what are they defined to be?
I mean how do they go into the geometry?
And I don't understand what
L = Height above valley bottom = Horizontal distance from valley bottom
means. Do you mean something like this:

?

 

[Sdtootle]

X and y would be your normal Cartesian coordinates which are not in your picture, but need to be.

Your description of L is correct.

 

[Redbelly98]

X and y would be your normal Cartesian coordinates which are not in your picture, but need to be.

I'll just add that the origin is located at the red dot at the bottom of the valley, and x & y refer to points along the white curve.

Your description of L is correct.

Yes.

 

[s0ft]

Thanks but I don't understand. If you could present your idea in a picture similar to mine, it could help a lot. I don't get how y/L=(x/L)^2

 

[Redbelly98]

That's a technique used to figure out the constant terms in an equation, when we already know the equation's general form. It's mostly a matter of manipulating the algebra.

We know that we are trying to express a parabola, with it's minimum point -- the red dot in your figure, or the bottom green dot in the figure below -- located at the origin (x=y=0). This is really the picture you drew already, but here is an example including x and y coordinates:

In general, every parabola like this can be expressed mathematically in the following form:
<br /> \frac{y}{\text{something}} = \left( \frac{x}{\text{something}} \right) ^2<br />
... and then we have to figure out what the two "somethings" are to get a final expression.

We have to know the value of some point on the parabola in order to plug numbers into the "somethings" above. The green dot at the upper right of the figure tells us that the point (x=8,y=16) is on the parabola, so we can use the 8 and 16 in the equation:

<br /> \frac{y}{16} = \left( \frac{x}{8} \right) ^2<br />
It's important to realize two things about the above equation:
1. It describes a parabola (due to the x² )
2. It is a correct equation for (x=8, y=16)

And doing some algebra, we get
\begin{align}<br /> y &amp;= 16\left( \frac{x}{8} \right) ^2 \\<br /> \\<br /> y &amp;= \frac{16}{8^2}x^2 =\frac{16}{64} x^2\\<br /> \\<br /> y &amp;= \frac{1}{4} x^2 \ \ \text{ or, equivalently, } \ \ y = 0.25 \ x^2<br /> \end{align}

So that is the equation of the parabola. By the way, you may notice that the point (4,4) is located on the parabola as well. So we could have used 4 for each "something", and we would have ended up with the same result. (In this example, the value of L would be 4.)

 

[s0ft]

Does the weight resolve into mgsinθcosθ in this way?

And you said tanθ=dy/dx but wasn't y the vertical length scale and x the horizontal according to the parabolic equation you explained? Still confused.
Thank you for the effort you're putting!

 

[Redbelly98]

x and y can refer to any point on the parabola, not just the point used to figure out the length scale.

See the attached figure, showing a parabola with length scale of 4. At the point (x,y), the parabola has some slope, as indicated by the black diagonal line.

θ is the angle of the sloping line from the horizontal. And tanθ gives the value of the slope, i.e. \frac{\Delta y}{\Delta x} or "rise over run".