gnits
- 137
- 46
- Homework Statement
- To find the closest approach of two ships
- Relevant Equations
- d=st
Could I please ask for help regarding the last part of this question:
At a given instant, a ship P revelling due east at a speed of 30km/h is 7km due north of a second ship Q which is traveling x degrees west of north at a speed of 14km/h, where tan(x)=3/4. Show that the speed of Q relative to P is 40km/h and find the direction of the relative velocity.
The ships continue to move with uniform velocities. Find:
a) The distance between the ships when they are nearest together.
b) The time taken, in minutes, to attain this shortest distance,
c) If initially, the course of Q had been altered to bring the ships as close as possible, the speed of Q and the speed and course of P being unchanged, find the direction of this new course.
I've done the first parts. It is part C that I feel must have a simpler way of being solved than the one I have. Here's me working for part C. First a diagram. to approach as closely as possible Q will need to head say x degrees east of north:
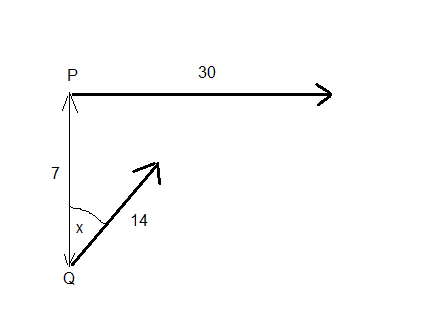
Let i and j be unit vectors in the directions east and north respectively.
The position vector of P at time t is:
##r_p=30ti##
The position vector of Q at time t is:
##r_q=14t\,sin(x)\,i + (14t\,cos(x)-7)\,j##
Therfore the position vector of Q relative to P is:
##r_{qp}=r_q-r_p=(14t\,sin(x)-30t)\,i+(14t\,cos(x)-7)\,j##
and so, the distance between P and Q (call this D) is given by:
##D^2=(196t^2sin^2x-840t^2sin(x)+900t^2)+(196t^2cos^2(x)-196t\,cos(x)+49)##
##= 1096t^2-840t^2sin(x)-196t\,cos(x)+49## Call this "Equation (1)"
and so ##\frac{d(D^2)}{dt}=(2192-1680\,sin(x))t-196cos(x)##
and so this is a minimum when:
##t=\frac{196\,cos(x)}{2192-1680sin(x)}=\frac{49\,cos(x)}{584-420\,sin(x)}##
So this is the time at which minimum distance occurs. Next I would have to substitute this value for t into equation (1) to obtain an expression for D^2 in terms of x only, and then choose x so as to minimise this.
Is there an easier way? (ths answer given in the book is x = arcsin(7/15) east of north).
Thanks,
Mitch.
At a given instant, a ship P revelling due east at a speed of 30km/h is 7km due north of a second ship Q which is traveling x degrees west of north at a speed of 14km/h, where tan(x)=3/4. Show that the speed of Q relative to P is 40km/h and find the direction of the relative velocity.
The ships continue to move with uniform velocities. Find:
a) The distance between the ships when they are nearest together.
b) The time taken, in minutes, to attain this shortest distance,
c) If initially, the course of Q had been altered to bring the ships as close as possible, the speed of Q and the speed and course of P being unchanged, find the direction of this new course.
I've done the first parts. It is part C that I feel must have a simpler way of being solved than the one I have. Here's me working for part C. First a diagram. to approach as closely as possible Q will need to head say x degrees east of north:
Let i and j be unit vectors in the directions east and north respectively.
The position vector of P at time t is:
##r_p=30ti##
The position vector of Q at time t is:
##r_q=14t\,sin(x)\,i + (14t\,cos(x)-7)\,j##
Therfore the position vector of Q relative to P is:
##r_{qp}=r_q-r_p=(14t\,sin(x)-30t)\,i+(14t\,cos(x)-7)\,j##
and so, the distance between P and Q (call this D) is given by:
##D^2=(196t^2sin^2x-840t^2sin(x)+900t^2)+(196t^2cos^2(x)-196t\,cos(x)+49)##
##= 1096t^2-840t^2sin(x)-196t\,cos(x)+49## Call this "Equation (1)"
and so ##\frac{d(D^2)}{dt}=(2192-1680\,sin(x))t-196cos(x)##
and so this is a minimum when:
##t=\frac{196\,cos(x)}{2192-1680sin(x)}=\frac{49\,cos(x)}{584-420\,sin(x)}##
So this is the time at which minimum distance occurs. Next I would have to substitute this value for t into equation (1) to obtain an expression for D^2 in terms of x only, and then choose x so as to minimise this.
Is there an easier way? (ths answer given in the book is x = arcsin(7/15) east of north).
Thanks,
Mitch.
Last edited: