- #1
Swagger
- 19
- 0
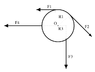
A uniform 2.9-kg cylinder can rotate about an axis through its center at O. The forces applied are: F1 = 2.4 N, F2 = 3.9 N, F3 = 6.1 N, and F4 = 4.6 N. Also, R1 = 11.2 cm and R3 = 4.0 cm. Find the magnitude and direction (+: counterclockwise; -: clockwise) of the angular acceleration of the cylinder. (see attachment)
I'm having a hard time with this one. I know that:
Torque (net) = Inertia * Angular Acceleration
and
Torque = Force * Radius
I've got:
T(F1)=0.2688 Nm
T(F2)=-0.4368 Nm
T(F3)=-0.0244 Nm
T(F4)=0 Nm
Tnet=-0.1924 Intertia=0.0181888
and the angular accerleration= -10.58 rad/s^2 (INCORRECT)
What am I doing wrong?
I'm having a hard time with this one. I know that:
Torque (net) = Inertia * Angular Acceleration
and
Torque = Force * Radius
I've got:
T(F1)=0.2688 Nm
T(F2)=-0.4368 Nm
T(F3)=-0.0244 Nm
T(F4)=0 Nm
Tnet=-0.1924 Intertia=0.0181888
and the angular accerleration= -10.58 rad/s^2 (INCORRECT)
What am I doing wrong?