adorfy
- 3
- 0
I've got 3 problems that I got wrong on my most recent test (college 1st year physics). I need to figure out what I did wrong and hopefully someone here can help me.
I know all my answers are wrong because I got marked wrong but I'm unsure why, or if there's another way or a better way to go about solving it.
Thank you for any help you can give.
[b]I. 1st problem[/b]
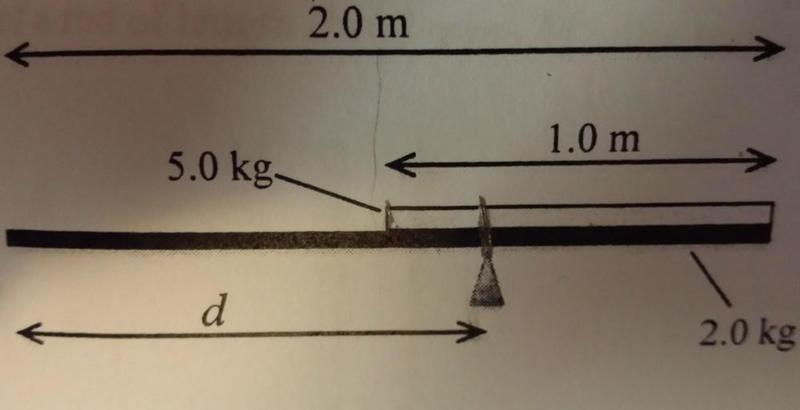
2 thin, uniform planks are balanced on a pivot.
The second plank is flush against the right end of the first.
The first is 2 meters long and weighs 1kg
The second is 1 meter long and has mass 5 kg
What is the distance from the left end of the first plank that the pivot must be placed?
τ=F*d
F = m*g
I know that the torque on the left of the pivot (counterclockwise) has to equal the torque on the right(clockwise) so I set up my equation to look like this:
F1 = m1*g
F2 = m2*g
(2-d)/1*F1+(2-d)/2*F2=(d-1)/1*F1+d/2*F2
simplified I got
d = (m2 +3*m1)/(m2+2*m1) = 17/12
[b]II. 2nd problem[/b]
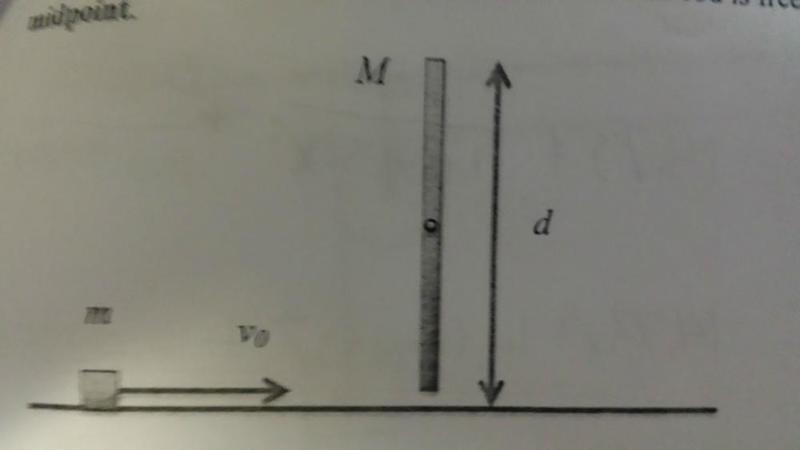
A solid cube slides without friction, it collides elastically with the end of a rod. The rod is free to rotate about an axis at it's midpoint
The cube has mass m
The cube slides at speed v0
The rod is length d
The rod is mass M
a. What does M have to be (in terms of the other variables) for the cube to come to rest as result of the collision
b. What is the angular speed of the rod immediately after the collision
m*v0=Iω
I= 1/12 * M * d^2 (for the rod)
I'm not actually sure if this is an actual equation and my error could be this simple. I know m*v is the formula for regular momentum and Iω is angular momentum so I believe that when they're equal that the cube should rest.
m*v0 = Iω
m*v0 = (1/12*M*d^2)*
M = (12*m*v0) / (d^2*)
[b]III. 3rd problem[/b]
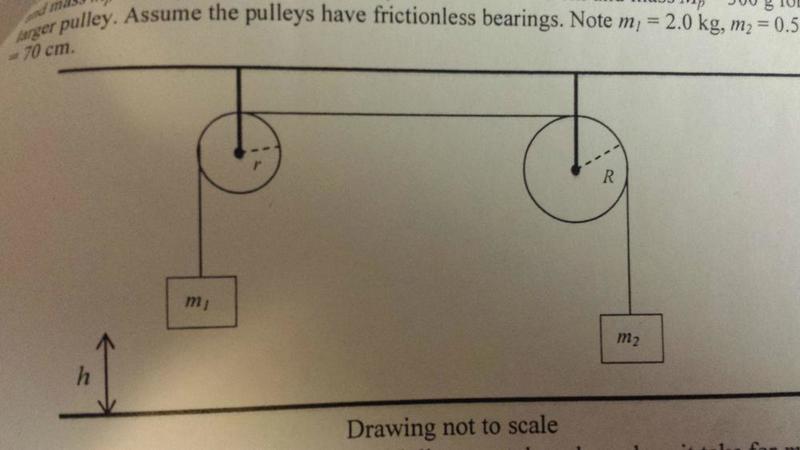
2 masses are connected by a frictionless rope run through 2 pulleys
m1 has mass 2 kg
m2 has mass 0.5 kg
@ t=0, m2 is 70 cm above the ground
pulley 1 has radius R of 8 cm and mass Mp of 800g
pulley 2 has radius r of 5 cm and mass mp of 200g
a. What is the time when m1 hits the ground?
b. What is the angular speed of the larger pulley (R=8 cm Mp=800g) when m1 hits the ground?
τ=F*d
F = m*a
a. I set up my equation like
am1 = (m1*g-(m2*g-FpulleyR-Fpulleyr))/m
FpulleyR= 1/2 * M* R^2 * ((h/(2∏R))/t^2) =( Mp*R^2*h)/(4∏Rt^2)
Fpulleyr= 1/2 * m* R^2 * ((h/(2∏r))/t^2) =( mp*r^2*h)/(4∏rt^2)
after plugging everything in and solving I got t = 0.435 seconds
b.
ω=Δ∅/t=h/2∏Rt=0.7/(2∏*0.08*0.435) = 3.201 rad/seconds
Like I said previously any help with any of these problems would be helpful. It's definitely possible I just made stupid mistakes in any or all of them and just don't realize it. Thank you
I know all my answers are wrong because I got marked wrong but I'm unsure why, or if there's another way or a better way to go about solving it.
Thank you for any help you can give.
[b]I. 1st problem[/b]
Homework Statement
2 thin, uniform planks are balanced on a pivot.
The second plank is flush against the right end of the first.
The first is 2 meters long and weighs 1kg
The second is 1 meter long and has mass 5 kg
What is the distance from the left end of the first plank that the pivot must be placed?
Homework Equations
τ=F*d
F = m*g
The Attempt at a Solution
I know that the torque on the left of the pivot (counterclockwise) has to equal the torque on the right(clockwise) so I set up my equation to look like this:
F1 = m1*g
F2 = m2*g
(2-d)/1*F1+(2-d)/2*F2=(d-1)/1*F1+d/2*F2
simplified I got
d = (m2 +3*m1)/(m2+2*m1) = 17/12
[b]II. 2nd problem[/b]
Homework Statement
A solid cube slides without friction, it collides elastically with the end of a rod. The rod is free to rotate about an axis at it's midpoint
The cube has mass m
The cube slides at speed v0
The rod is length d
The rod is mass M
a. What does M have to be (in terms of the other variables) for the cube to come to rest as result of the collision
b. What is the angular speed of the rod immediately after the collision
Homework Equations
m*v0=Iω
I= 1/12 * M * d^2 (for the rod)
I'm not actually sure if this is an actual equation and my error could be this simple. I know m*v is the formula for regular momentum and Iω is angular momentum so I believe that when they're equal that the cube should rest.
The Attempt at a Solution
m*v0 = Iω
m*v0 = (1/12*M*d^2)*
M = (12*m*v0) / (d^2*)
[b]III. 3rd problem[/b]
Homework Statement
2 masses are connected by a frictionless rope run through 2 pulleys
m1 has mass 2 kg
m2 has mass 0.5 kg
@ t=0, m2 is 70 cm above the ground
pulley 1 has radius R of 8 cm and mass Mp of 800g
pulley 2 has radius r of 5 cm and mass mp of 200g
a. What is the time when m1 hits the ground?
b. What is the angular speed of the larger pulley (R=8 cm Mp=800g) when m1 hits the ground?
Homework Equations
τ=F*d
F = m*a
The Attempt at a Solution
a. I set up my equation like
am1 = (m1*g-(m2*g-FpulleyR-Fpulleyr))/m
FpulleyR= 1/2 * M* R^2 * ((h/(2∏R))/t^2) =( Mp*R^2*h)/(4∏Rt^2)
Fpulleyr= 1/2 * m* R^2 * ((h/(2∏r))/t^2) =( mp*r^2*h)/(4∏rt^2)
after plugging everything in and solving I got t = 0.435 seconds
b.
ω=Δ∅/t=h/2∏Rt=0.7/(2∏*0.08*0.435) = 3.201 rad/seconds
Like I said previously any help with any of these problems would be helpful. It's definitely possible I just made stupid mistakes in any or all of them and just don't realize it. Thank you