- #1
frozen7
- 163
- 0
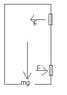
A door 2.30m high and 1.30m wide,has a mass of 13.0kg. A hinge 0.40m from the top and another hinge from the bottom each support half the door`s weight. By assumming that the center of gravity is at the geometrical center of the door,determine the horizontal and vertical force components exerted by each hinge on the door.
How to solve this question? I have no idea at all to start doing.
How to solve this question? I have no idea at all to start doing.