APool555
- 15
- 0
We just started torque and our teacher gave us some problems but we didn't do any examples. I have no idea where to start. Thanks for your help.
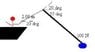
The fishing pole in Figure P10.30(i drew a picture of it) makes an angle of 20 degrees with the horizontal. What is the torque exerted by the fish about an axis perpendicular to the page and passing through the fishers hand?
The fishing pole in Figure P10.30(i drew a picture of it) makes an angle of 20 degrees with the horizontal. What is the torque exerted by the fish about an axis perpendicular to the page and passing through the fishers hand?