subbby
- 22
- 0
What I have ?
What I need ?
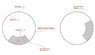
Want to Calculate the torque required to move that solid circular sector from the intial position to the position shown in attached picture (90 Degrees rotation)
Data :
What I have caluted ?
How do I proceed ?
- Have a 16’ x 72’ rotating drum
- There is a solid circular sector inside the drum
What I need ?
Want to Calculate the torque required to move that solid circular sector from the intial position to the position shown in attached picture (90 Degrees rotation)
Data :
- RPM = 10
- time = 15 seconds
What I have caluted ?
- Calculated the torque required to rotate the drum using Torque = Moment of Inertia X Alpha where Alpha = angular acceleration
How do I proceed ?
- Do I have to calculate the moment of inertia of that solid circular sector and then use the same formula?
- But here its not a complete rotation. Its just 90 degrees. So how to arrive at torque to move a mass about an axis only to a certain degree?
- Or, Should it be just Torque = Force * Radius ? where force shall be its mass * acceleration due to gravity and radius shall be distance from the drum's rotation axis to the circular sector's center of gravity ?
- Does Perpendicular axes theorem or Parallel Axes theorem come into the picture ?