NYC2LA
- 8
- 0
I am NOT a physics major and clueless to figure out the strength of a custom spring I need to be made. I was hoping someone could help me, either with figuring it out, or turning me to someone/site that may be able to help.
Here's the sitch':
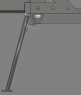
The spring is for a center kick-stand on a bicycle. The kick-stand/frame is custom built.
The spring must be a torsion spring.
the total weight of the kick-stand (placed on a scale) is 12 ounces.
The spring should have enough torsional strength to keep the kick-stand in its non-deployed position (up, riding the bike) and keep it there with extra forces of being thrust on it by bumpy roads, etc.
Make sense?
Please help, and thank you in advance!
Here's the sitch':
The spring is for a center kick-stand on a bicycle. The kick-stand/frame is custom built.
The spring must be a torsion spring.
the total weight of the kick-stand (placed on a scale) is 12 ounces.
The spring should have enough torsional strength to keep the kick-stand in its non-deployed position (up, riding the bike) and keep it there with extra forces of being thrust on it by bumpy roads, etc.
Make sense?
Please help, and thank you in advance!