Etech_Soffy
- 3
- 0
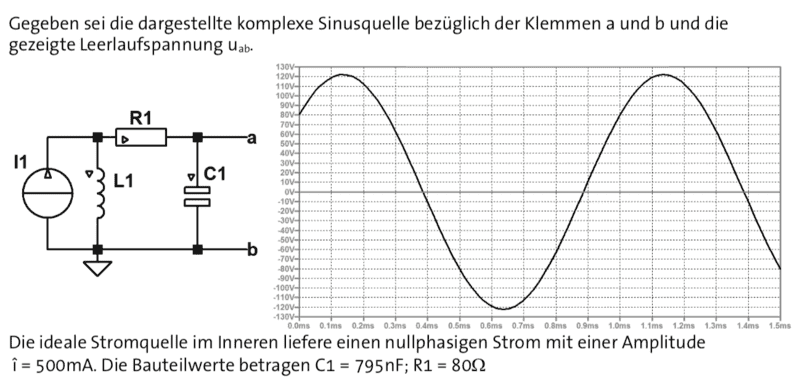
Summary:: So the question is, what do I need to do on clamp 'ab', so that the total current only goes through the Inductor L1.
I know the must be a second inductor parallel to the capacitor C1, but i don't know why.
Can someone please explain.
I also included the german question under the picture.

I know the must be a second inductor parallel to the capacitor C1, but i don't know why.
Can someone please explain.
I also included the german question under the picture.