Understanding Coordinate Transformation of a Tensorial Relation

[Arman777]

Let us suppose we have a covariant derivative of a contravariant vector such as

$$\nabla_{\mu}V^{\nu}=\partial_{\mu}V^{\nu} + \Gamma^{\nu}_{\mu \lambda}V^{\lambda}$$

If $\Delta_{\mu}V^{\nu}$ is a (1,1) Tensor, it must be transformed as

$$\nabla_{\bar{\mu}}V^{\bar{\nu}} = \frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}\nabla_{\mu}V^{\nu}$$

Or

$$\nabla_{\bar{\mu}}V^{\bar{\nu}} = \frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}[\partial_{\mu}V^{\nu} + \Gamma^{\nu}_{\mu \lambda}V^{\lambda}]$$

Now my question is does $\frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}$ acts a differential or it acts like a multiplication on the $[\partial_{\mu}V^{\nu} + \Gamma^{\nu}_{\mu \lambda}V^{\lambda}]$ ?

So which of these expressions is true

1) $$\frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}(\partial_{\mu})V^{\nu} + \frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}(V^{\nu} )\partial_{\mu} + \frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}(\Gamma^{\nu}_{\mu \lambda}) V^{\lambda}+ \frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}(V^{\lambda})\Gamma^{\nu}_{\mu \lambda}$$

2)$$\frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}\partial_{\mu}V^{\nu} + \frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}\Gamma^{\nu}_{\mu \lambda}V^{\lambda}$$

In principle the correct equation need to be 1 I guess but I cannot be sure somehow.

I am was doing inverse operations of these equations (showing that $\nabla_{\bar{\mu}}V^{\bar{\nu}}$ transforms as a tensor) and I have obtained something like this

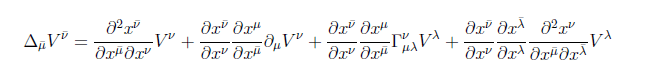
There are extra two terms which I cannot explain why are they. The only logical explanation seemed to be that the $\frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}$ must act as a differential operation on $[\partial_{\mu}V^{\nu} + \Gamma^{\nu}_{\mu \lambda}V^{\lambda}]$

 

[etotheipi]

$\frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}$ is just a number and not a differential operator, so you should absolutely not 'apply Leibnitz' like you've done in option (1)!

 

[Orodruin]

(2) - the differential operator is acting on $V$.

Also, careful with $\nabla$ vs $\Delta$.

 

[Arman777]

I was doing these calculations

and the first and the last terms seems extra. Are they 0 or am I missing something in this derivation ? Thats actually why I asked this question but it seems I am doing something wrong..

As you know to show $\nabla_{\bar{\mu}}V^{\bar{\nu}}$ transforms as a tensor I need to write it as $$\nabla_{\bar{\mu}}V^{\bar{\nu}} = \frac{ \partial x^{\bar{\nu}}}{\partial x^\nu}\frac{\partial x^{\mu}}{\partial x^{\bar{\mu}}}\nabla_{\mu}V^{\nu}$$ which I cannot do at this moment

 

[etotheipi]

Although they were a little sloppy re-using the index $\lambda$ in their fourth line of equations, the working in the image looks okay? I have the feeling the first of those terms vanishes, because
$$\cancel{\frac{\partial^2 x^{\bar{\nu}}}{\partial x^{\bar{\mu}} \partial x^{\nu}} = \frac{\partial^2 x^{\bar{\nu}}}{ \partial x^{\nu} \partial x^{\bar{\mu}}} = \frac{\partial}{\partial x^{\nu}} \delta^{\bar{\nu}}_{\bar{\mu}} = 0}$$however I don't know how to show the second of those terms vanishes. Let's hope someone gives a hint!

 

[Arman777]

Although they were a little sloppy re-using the index λ in their fourth line of equations,

That is my typing. I did those calculations.

however I don't know how to show the second of those terms vanishes. Let's hope someone gives a hint!

Yeah I could not see a mistake either. I am kind of stuck here

 

[Orodruin]

I suggest not writing things like
$$
\frac{\partial^2 x^{\bar \nu}}{\partial x^{\bar \mu} \partial x^\nu}
$$
with derivatives that are using different coordinates as they generally do not commute. What you want to write is instead something like
$$
\partial_{\bar \mu} \frac{\partial x^{\bar \nu}}{\partial x^\nu}
$$
as it is much clearer what is intended.

I suggest you do the following:

1. Rename the dummy index $\nu$ in the first term to $\lambda$. This will allow you to factor out $V^\lambda$ from the superfluous terms.
2. Note that $$\frac{\partial^2 x^\nu}{\partial x^{\bar \mu} \partial x^{\bar \lambda}} \frac{\partial x^{\bar \lambda}}{\partial x^\lambda} = \partial_{\bar \mu}\left( \frac{\partial x^\nu}{\partial x^{\bar \lambda}} \frac{\partial x^{\bar \lambda}}{\partial x^\lambda} \right) - \frac{\partial x^\nu}{\partial x^{\bar \lambda}} \partial_{\bar\mu} \frac{\partial x^{\bar \lambda}}{\partial x^\lambda}$$ and go from there.

 

[Orodruin]

Although they were a little sloppy re-using the index $\lambda$ in their fourth line of equations, the working in the image looks okay? I have the feeling the first of those terms vanishes, because$$\frac{\partial^2 x^{\bar{\nu}}}{\partial x^{\bar{\mu}} \partial x^{\nu}} = \frac{\partial^2 x^{\bar{\nu}}}{ \partial x^{\nu} \partial x^{\bar{\mu}}} = \frac{\partial}{\partial x^{\nu}} \delta^{\bar{\nu}}_{\bar{\mu}} = 0$$however I don't know how to show the second of those terms vanishes. Let's hope someone gives a hint!

No, the derivatives do not commute, this is precisely what I warned about in #7.

 

[Arman777]

I suggest not writing things like
$$
\frac{\partial^2 x^{\bar \nu}}{\partial x^{\bar \mu} \partial x^\nu}
$$
with derivatives that are using different coordinates as they generally do not commute. What you want to write is instead something like
$$
\partial_{\bar \mu} \frac{\partial x^{\bar \nu}}{\partial x^\nu}
$$
as it is much clearer what is intended.

I suggest you do the following:

1. Rename the dummy index $\nu$ in the first term to $\lambda$. This will allow you to factor out $V^\lambda$ from the superfluous terms.
2. Note that $$\frac{\partial^2 x^\nu}{\partial x^{\bar \mu} \partial x^{\bar \lambda}} \frac{\partial x^{\bar \lambda}}{\partial x^\lambda} = \partial_{\bar \mu}\left( \frac{\partial x^\nu}{\partial x^{\bar \lambda}} \frac{\partial x^{\bar \lambda}}{\partial x^\lambda} \right) - \frac{\partial x^\nu}{\partial x^{\bar \lambda}} \partial_{\bar\mu} \frac{\partial x^{\bar \lambda}}{\partial x^\lambda}$$ and go from there.

Let me try that, thanks for the info

 

[etotheipi]

Ah, I think I got it with the hint! @Orodruin why don't the partial derivatives with respect to different coordinates commute?

 

[Arman777]

I get this..

Can we eliminate $\partial x^{\bar{\lambda}}$ and write

otherwise I am stuck.

 

[Orodruin]

Ah, I think I got it with the hint! @Orodruin why don't the partial derivatives with respect to different coordinates commute?

Because the commutation of the partial derivatives requires that the derivatives are taken with respect to independent variables. This is easiest to see in one dimension with coordinates $x$ and $y$, respectively:
$$
\frac{d}{dx} \frac{df}{dy} = \frac{d}{dx}\left(\frac{dx}{dy} \frac{df}{dx}\right)
= \frac{dx}{dy} \frac{d^2 f}{dx^2} + \frac{df}{dx} \frac{d}{dx} \frac{dx}{dy}
= \frac{d}{dy} \frac{df}{dx} + \frac{df}{dx} \frac{dy}{dx} \frac{d^2 x}{dy^2}.
$$
In other words, the commutator of the derivatives is non-zero if the second derivative of the coordinate transformation is non-zero.

Edit: For the general n-dimensional case you will have to add a lot of indices, but the general idea remains the same.

 

[Orodruin]

I get this..
View attachment 281074
Can we eliminate $\partial x^{\bar{\lambda}}$ and write
View attachment 281075
otherwise I am stuck.

That's just applying $\partial x^{\bar\nu}/\partial x^{\bar \lambda} = \delta^{\bar\nu}_{\bar \lambda}$ (alternatively, the chain rule).

 

[Arman777]

That's just applying $\partial x^{\bar\nu}/\partial x^{\bar \lambda} = \delta^{\bar\nu}_{\bar \lambda}$ (alternatively, the chain rule).

I see. Since $$\partial_{\bar{\mu}}(\frac{\partial x^{\bar{\lambda}}}{\partial x^{\lambda}})\frac{\partial x^{\bar{\nu}}}{\partial x^{\bar{\lambda}}}$$ I thought we may not apply it here. So the problem is solved I guess. Thank you all for the help

Note: For instance if I not write $\delta^{\bar{\nu}}_{\bar{\lambda}}$ and just cancel is it wrong?

 

[Orodruin]

I see. Since $$\partial_{\bar{\mu}}(\frac{\partial x^{\bar{\lambda}}}{\partial x^{\lambda}})\frac{\partial x^{\bar{\nu}}}{\partial x^{\bar{\lambda}}}$$ I thought we may not apply it here. So the problem is solved I guess. Thank you all for the help

If that is what you got then you got something different from me. I would expect both of the derivatives to be acted upon by the $\partial_{\bar\mu}$. Can you post your work?

 

[Arman777]

If that is what you got then you got something different from me. I would expect both of the derivatives to be acted upon by the $\partial_{\bar\mu}$. Can you post your work?

 

[Orodruin]

Right, sorry. It is still using that $\partial x^{\bar \nu}/\partial x^{\bar\lambda} = \delta^{\bar\nu}_{\bar\lambda}$, which is a constant that can be freely moved inside the derivative. It is, however, not using the chain rule.

 

[Arman777]

Right, sorry. It is still using that $\partial x^{\bar \nu}/\partial x^{\bar\lambda} = \delta^{\bar\nu}_{\bar\lambda}$, which is a constant that can be freely moved inside the derivative. It is, however, not using the chain rule.

Okay then, nice.