Transformer N1V1=N2V2 works only one freq

[Albertgauss]

TL;DR Summary

For a lab transformer, I can only get V2/V1 = N2/N1 to be valid at one frequency. However, in Phys Calc Sem 2, a whole section is treated on this subject, and it seems this expression should be valid at all freqs. Why is Vs/Vp = Ns/Np only valid at one, single freq?

Hi all,
Recently, I have been playing around with the Pasco Transformer Demo set of SF-8616. I have been trying to verify the transformer relationship

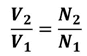
where the "2"s mean secondary and "1's" mean primary. However, no matter what configuration I try, this relationship holds at a single frequency only. It does not hold true at almost any other frequency except for one--what appears to be--resonant frequency. Why does this relationship hold only at a single frequency when you test out a transformer in real life? Shouldn't this formula hold for a wide range of frequencies? Since this relationship only seems to be valid at one single frequency, why is it taught as such a general principle in many semester 2 calculus/engineering science courses?

The primary is input with a sine wave from a Tektronix Function Generator AFG 1022 of about 2.0 volts peak-peak (which doesn’t always mean 2 volts peak-peak on the oscilloscope). I measure both waveforms from the primary and secondary (labelled 2ndary) with a Tektronix TDS 1002B oscilloscope. The step-up transformers I have tried are A) 200 turns to 400 turns, B) 200 to 800 turns, and C) 400 to 800 turns. I tried the following configurations in the picture: Configs_Tried.jpg

In each configuration I went from 100 Hertz to 500,000 Hertz. Usually, the single frequency in which the transformer relationship above held occurred somewhere between 50,000 and 200,000 Hertz. The best working configuration (see the file above "Configs_Tried.jpg" for what my transformer labels mean) for this result was when the two coils shared just a “Ferrous Core” between them; neiither the “Air Core” or “Square Arrangement” worked very well for verifying the transformer relationship above. Below, you can see the only frequency for the “Ferrous Core” configuration at a frequency of 121,000 Hertz in which the transformer relationship above holds in the file: "OutputScopeTrans,jpg"

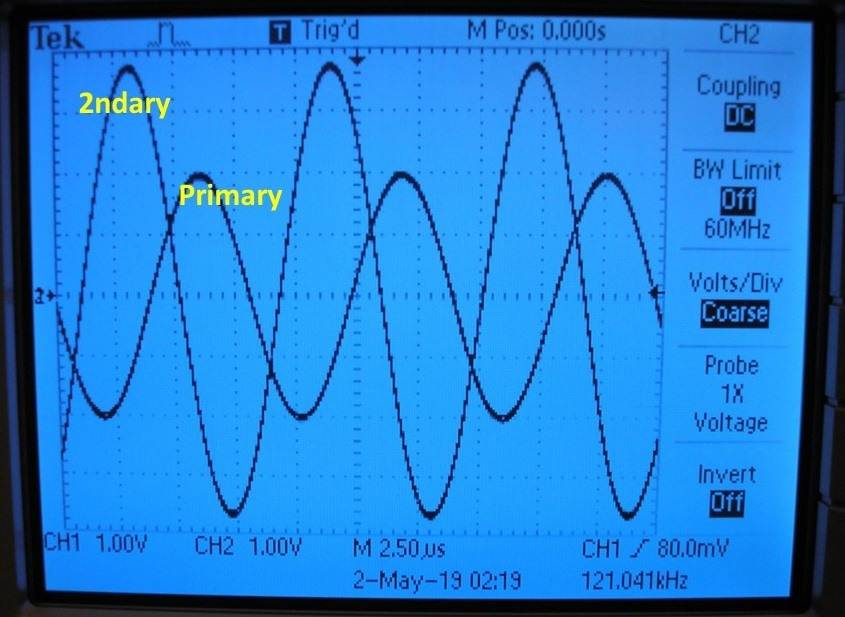
The circuit does behave like an LRC circuit where the single frequency at which the transformer relationship holds acts like a resonance frequency. My guess is there a capacitor in the scope somewhere (as has happened before) but shouldn’t the oscilloscope know how to nullify its effect in a circuit when someone is trying to make an objective measurement?

I could not find, but does anyone know of a more advanced transformer relationship then the one I listed above but that has frequency dependence and explain my outcomes a little better?

 

[gleem]

You might start with asking yourself what are the assumptions made to derive the "transformer equation" and how does that compare with a real world transformer. Are the assumptions good? How good.

 

[Albertgauss]

The proof is in any standard physics with calculus textbook for engineering majors. Basically, in Young and Freedman, University Physics, I attach the following proof. It looks like every book at this level offers the same proof.

That is, by sharing the bar magnet in this "square configuration", the flux changing through one arm is the same as the flux changing through the other arm of the transformer, and that yields the "transformer equation" I began in this post. However, this configuration did not work well when I actually tried it. Note that there is nothing about frequency limitations in this (way-too) simple proof.

But I do know that transformers ARE used. What is different about a real transformer and the Pasco coils I use here (which are used for physics demonstrations)? Do real transformers in use have the same problem that they only work for a single frequency (and are thus, fine-tuned for that only frequency), or do in-use transformers have a frequency band in which they work well over many frequencies? If anyone knows where I can get more reliable transformers that the "transformer equation" holds, let me know.

 

[willem2]

But I do know that transformers ARE used. What is different about a real transformer and the Pasco coils I use here (which are used for physics demonstrations)? Do real transformers in use have the same problem that they only work for a single frequency (and are thus, fine-tuned for that only frequency), or do in-use transformers have a frequency band in which they work well over many frequencies?

From the web page.

Note:
These are not ideal transformers. As is true for any transformer using separate coils (coils that are not coaxially wound on the same core), the flux linkage between coils is only about 10%. The voltage transformation ratios are therefore proportionately below the ideal values based on the number of turns per coil. Within this limitation, effective quantitative investigations can be conducted using these coil and core sets.

I'd expect the coils are probably meant to be used with power-line frequency. 50 or 60 Hz. The best results would no doubt be with the metal core. At the frequency you use it the output impedance must be really high, and the output voltage would likely mostly disappear with a realistic load.
Many transformers are only designed for those frequencies. Audio transformers do exist however. 500 kHz is well above the maximum frequency however. You might hope for the -3dB point (50% power) at 20 kHz. Higher frequency transformers need lower inductances, and a ferrite core, which won't conduct eddy currents.

 

[Asymptotic]

If anyone knows where I can get more reliable transformers that the "transformer equation" holds, let me know.

It isn't a problem of the transformer equation not holding, but rather that a lot of 'real world' goes into the Φ_B number that must be accounted for.

A copy of "Transformer Design Principles" or an equivalent ought to be in your school library.
https://archive.org/details/TransformerDesignPrinciples/page/n65

 

[berkeman]

From the web page.

Note:
These are not ideal transformers. As is true for any transformer using separate coils (coils that are not coaxially wound on the same core), the flux linkage between coils is only about 10%.

From which web page? 10% is terrible mutual coupling! For most transformers, the leakage inductance Lk is significantly lower than the magnetizing inductance Lm.

 

[willem2]

From which web page? 10% is terrible mutual coupling! For most transformers, the leakage inductance Lk is significantly lower than the magnetizing inductance Lm.

https://www.pasco.com/prodCatalog/SF/SF-8616_basic-coil-set/index.cfm
I'd have tought it would be more than that too, at least if you use a metal core.