- #1
nearc
Gold Member
- 66
- 6
Traveling signal “paradox”
Most relativity paradoxes are not true paradoxes they merely require some clarification about frame of references, stationary observer, etc… I hope some folk could help me clarify my “paradox” or point out where someone as already discussed this concept.
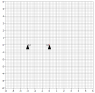
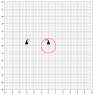
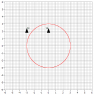
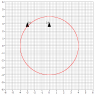
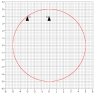
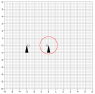
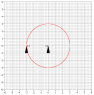
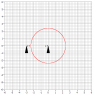
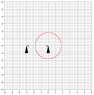
We have two ships on parallel vectors [see thumbnail, is there a better way to add images?], one ship [on the right] sends out a signal at step 0 [from the front tip of the ship] traveling the speed of light and that signal will eventually be picked up by the other ship [on the left] again the receiver is in the front tip. If the two ships are stationary then the signal will be received at step 4 denoted by the pair of white ships, however if the two ships are traveling at near light speed the receiving ship will not pick up the signal until step 9. If we say they are traveling near light speed but are not moving relative to anything then conventional wisdom dictates we treat them as stationary but this is where I am confused; how do we say the signal will be received in step 4 when it seems like it should be received in step 9?
Some notes about the diagram: Obviously using a band to show the propagation of a signal is not very accurate. Also I attempted to show the ships traveling slightly slower than the signal propagation. At step 0 the broadcasting ship front tip was in the middle of the band, whereas, in step 9 it was at the edge of the band. Hopefully the general idea can be gleamed.
Most relativity paradoxes are not true paradoxes they merely require some clarification about frame of references, stationary observer, etc… I hope some folk could help me clarify my “paradox” or point out where someone as already discussed this concept.
We have two ships on parallel vectors [see thumbnail, is there a better way to add images?], one ship [on the right] sends out a signal at step 0 [from the front tip of the ship] traveling the speed of light and that signal will eventually be picked up by the other ship [on the left] again the receiver is in the front tip. If the two ships are stationary then the signal will be received at step 4 denoted by the pair of white ships, however if the two ships are traveling at near light speed the receiving ship will not pick up the signal until step 9. If we say they are traveling near light speed but are not moving relative to anything then conventional wisdom dictates we treat them as stationary but this is where I am confused; how do we say the signal will be received in step 4 when it seems like it should be received in step 9?
Some notes about the diagram: Obviously using a band to show the propagation of a signal is not very accurate. Also I attempted to show the ships traveling slightly slower than the signal propagation. At step 0 the broadcasting ship front tip was in the middle of the band, whereas, in step 9 it was at the edge of the band. Hopefully the general idea can be gleamed.