Kolika28
- 146
- 28
Homework Statement
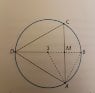
In a circle with center S, DB is the diameter. The line AC goes 90 degrees from the center point M of the line SB. "
What type of triangle is ACD?
2. Homework Equations
The Attempt at a Solution
I can see it is an equilateral triangle, but do not know how to explain it. I know it has something to do with the center of the circle S. I believe it may have something to do with the line SM as it goes through the midpoint of the side AS. But I do not know what to do after this, I'm really lost.
I really appreciate some help :)
Attachments
Last edited: