You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Trig idents while computing limit
Physics news on Phys.org
- 2,009
- 974
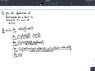
I was able to work through that step using $$cos(x+y)=cos(x)cos(y)-sin(x)sin(y)$$ and $$sin(x+y)=sin(x)cos(y)+cos(x)sin(y)$$
See this link:
http://www.mathwords.com/t/trig_identities.htm
See this link:
http://www.mathwords.com/t/trig_identities.htm
quicksilver123
- 173
- 0
That is the identity I used to expand the (x+h) terms but could not factor to the next step due to the sin(h) term... unless I made an error in my expansion that I haven't caught?
- 2,009
- 974
In your work, factor a sin(x) from the first 2 terms and cos(x) from the next 2 terms. You should now have the same as the solution guide. Note that it takes 2 lines to display theirs. I don't know what you've done in the denominator, though. .
quicksilver123
- 173
- 0
Thanks. I don't know why I didn't see that.
There are two things I don't understand about this problem. First, when finding the nth root of a number, there should in theory be n solutions. However, the formula produces n+1 roots. Here is how. The first root is simply ##\left(r\right)^{\left(\frac{1}{n}\right)}##. Then you multiply this first root by n additional expressions given by the formula, as you go through k=0,1,...n-1. So you end up with n+1 roots, which cannot be correct. Let me illustrate what I mean. For this...
Hello,
This is the attachment, the steps to solution are pretty clear. I guess there is a mistake on the highlighted part that prompts this thread.
Ought to be ##3^{n+1} (n+2)-6## and not ##3^n(n+2)-6##. Unless i missed something, on another note, i find the first method (induction) better than second one (method of differences).
Similar threads
- Replies
- 4
- Views
- 1K
- Replies
- 2
- Views
- 981
- Replies
- 27
- Views
- 3K
- Replies
- 2
- Views
- 2K
- Replies
- 10
- Views
- 1K
- Replies
- 5
- Views
- 2K
- Replies
- 14
- Views
- 1K
- Replies
- 5
- Views
- 1K
- Replies
- 2
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 96
- Calculus and Beyond Homework Help
-
Solving the wave equation with piecewise initial conditions
- Started by songoku
- Replies: 11
- Calculus and Beyond Homework Help
-
Area of loop in x-y plane
- Started by littlemathquark
- Replies: 20
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math