I decided to show the easy way to design a synchronous counter. Remember, that in order to be synchronous, not only must its counts up be synchronous, but also must the count which carries over and back to the initial value. The first thing that we should do, is to make up a 'truth table' for all the possible count values. There are four variables that will always determine what the next count must be --- the four "Q" outputs from the four flip-flops that hold the count values. (Actually, there are five, if the 'count clock' is considered, however since the flip-flops here can be driven in a "toggle" manner, just by controlling the "J" and "K" inputs to these flip-flops, --- then the "clock" can be ignored, since it won't control directly these control signals to the "J" and "K". Whenever both "J" and "K" are 'one' to any flip flop, it will toggle, [at the next clock] so we simply must decide for each flip-flop, when it must be 'one' at both "J" and "K". [all other times, it will be 'zero' at both of these inputs, so that nothing will happen then.])
In the first attachment, is drawn a 4-variable 'truth table'. Given in addition, is the 'decimal' equivalent for the sixteen values of four flip-flop outputs, just to make it easier to keep track of where we are. We note that, since count values "0", "13", "14" and "15" will not be used, these are shaded out.
Next, we draw "parallel" tables for the control inputs to each of the flip-flops. Here, I have left out a table set for the "A" flip-flop, because it is a trivial case. It toggles every time, so its inputs are just tied to "one" (+5Vdc). Each of the remaining three parallel tables then has two columns, --- one for when the conditions needed for a "toggle" must be present, and one for the direction for the toggle. Actually, the "Dir" columns aren't absolutely necessary, but they make it more convenient, for two reasons. First, they can represent the exact relative times of the toggles, and second, they give us an indication that we haven't screwed up (by not always following a 'down toggle' with an 'up toggle' and vice versa).
For the table of each needed output, we then put in an up or a down arrow at the point that the corresponding flip-flop must toggle. We put it across the "transition to the 'new state' because that is when the toggle must occur. If each up is followed by a "down" and each "down" by an "up", we are fairly sure that we have it right. Next, for each arrow, we put in a check (or the like). Here, we take care to put in the checks into the rows 'just ahead' of the anticipated toggles, because it is the "prior-state" conditions that control the toggles. (In essence, the "before-toggle" states are the (A, B, C and D) states of the flip-flops, while, the "after-toggle" states of each flip-flop can be called A", B", C" or D". Thus, we are looking for the A, B, C and D inputs that will give us the A", B", C" and D" flip-flop states. From this, we note that D->D" has two toggles per count cycle, C->C" has four and B->B" has six. ("A->A" naturally will have twelve, because it toggles every cycle.)
The next step, is to enter the table values into a K-Map for each variable. Here, we show only for C" and D", because B" (similar to A") is very simple, and should be obvious. If "ordered" K-Maps, like the ones shown in attachment-one are used then, filling the maps is easy, because the values from each table column can simply be put into a corresponding "cell" of its map. (Each is numbered.) For each checked location in a table column, put a "one" (or whatever is desired) into the corresponding map cell.
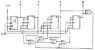
Next, we simply solve each K-Map to determine what the input logic to each count flip-flop must be. Note that several values of the original truth table are "forbidden" and thus will never occur (0, 13, 14 and 15). These are shown shaded in the maps. These can be used as 'don't care' states when the maps are solved --- thus they may be considered as either "zero" or "one"; whichever is convenient. Thus, when each map is solved, we get: A" = 1 (Every clock cycle) B" = A, C" = AB + CD and D" = ABC +CD.
Using the solutions derived, we can get a circuit like the one in attachment 2. (We could also use four NANDs and an Inverter.)
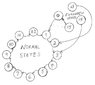
Finally, we should run through each state to verify what the transitions will be. Attachment 3 shows these transitions. We note that a power spike or something like it could put the counter, like any counter, into a "forbidden state (like any clock when the power is lost).This figure shows what would happen in such case. The circuit doesn't stay in the forbidden state, but , of course, count reference would be lost until the counter is re-initialized. We also note, that the counter that we have designed is basically like that of the standard twelve-hour time-of-day clock.
I hope that this has been useful. This method can be used with basically any synchronous sequencer/counter. Tomorrow (or the next day) I shall probably bring another example
--- an "Excess-three" counter.
KM