Troxx
- 2
- 0
- TL;DR Summary
- Trouble with infinity and complex numbers, just curious.
Summary: Trouble with infinity and complex numbers, just curious.
I'm not too familiar with set theory ... but <-∞, ∞> contains just real numbers?
Does something similar to <-∞, ∞> exist in Complex numbers?
My question, is it "wrong"?
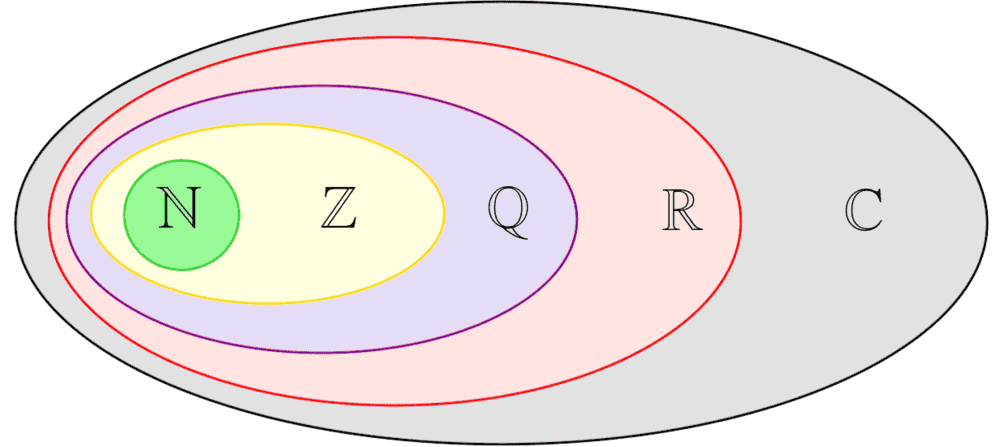
I'm not too familiar with set theory ... but <-∞, ∞> contains just real numbers?
Does something similar to <-∞, ∞> exist in Complex numbers?
My question, is it "wrong"?