Troubleshooting a Physics Problem: Where is the Flaw?

[lerngen]

Homework Statement

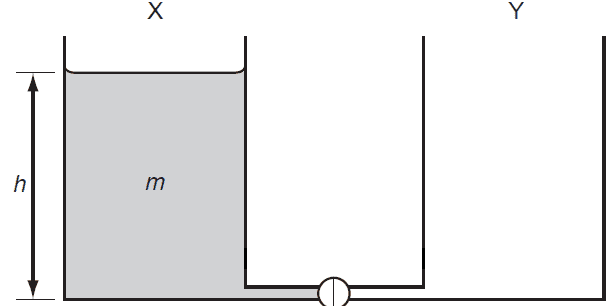
The diagram shows two identical containers, X and Y, that are connected by a thin tube of negligible volume. Initially container X is filled with water of mass 'm' up to a height 'h' and Y is empty.

[IMG]https://www.physicsforums.com/attachments/problem-png.252768/?hash=c542de39b0a9c79f411453b2931feac5[/IMG]

The valve is then opened and both containers contain equal quantities of water. The loss of gravitational potential
energy of the water is?

Relevant Equations

Energy_potential = mass*gravity*height

The image doesn't seem to be appearing in the problem statement so here it is:

I already know the correct answer and the method to arrive at it. However, I didn't find it very satisfying. So in attempting to create an answer that was, imo, more intuitively satisfying I:

a. treated the container as two parts
b. divided the containers into discreet rows of water spaced at integer height levels (h, h-1, h-2, ...h = 0) with center of gravity being at h + 0.5 levels
c. calculated the gravitational potential energy (Egrav) of each row and summed to get the original amount of Egrav for first side of the container
d. moved each row one by one to the other container
e. at the end, calculated the Egrav of each half of the container, added them together and compared to the original amount
f. I keep ending up with the lost gravitational energy being 1/2 the starting amount instead of the correct answer of 1/4 the starting amount.

Image demonstrating the general idea of what I am describing:

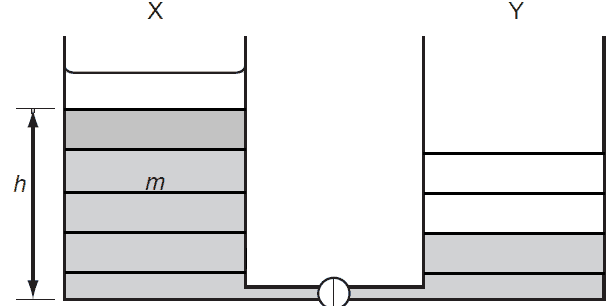
tl;dr - To summarize the entire process, first half of the container loses half of its mass and half of its height (1/4 * Egrav) which is a loss of 3/4 of the starting amount. The 2nd half of the container gains half the mass and half the height (1/4 * Egrav).

Thus -3/4 loss + 1/4 gain -> -2/4 -> -1/2 loss of starting amount. This does not match the correct answer of mgh/4 that is in the book and I've found online.

I feel like I've been staring at this too long and very likely missing something very obvious but I'll ask anyway. Where is the flaw in my physics thinking here? Thanks for your time.

 

[BvU]

Hello Lerngen, $\qquad$ $\qquad$ !

first half of the container loses half of its mass and half of its height

Correct. Potential energy goes from $mg{h\over2}$ to ${1\over 2}mg{h\over4}$
The other side gets ${1\over 2}mg{h\over4}$, so the difference is $mg{h\over4}$ and that is half the initial potential energy. Everybody happy

(your starting amount is not $mgh$ but $mg{h\over2}$ : the average height counts.

 

[Doc Al]

Thus -3/4 loss + 1/4 gain -> -2/4 -> -1/2 loss of starting amount. This does not match the correct answer of mgh/4 that is in the book and I've found online.

mgh/4 is the final PE. Compare that to the initial PE.

 

[BvU]

eq aequo !

 

[lerngen]

@BvU, Doc Al - Thanks for the welcome and response. I do understand that approach to getting the answer but if I apply that to individual blocks of water I do not get the same answer.

Some numbers:

1. Let 'h' = 6
2. Divide container 'X' and 'Y' into 6 individual containers of water (c1, c2, ...cN...c6), each weighing 1kg
3. The average height of each container 'cN', will be h - 0.5
4. Calculating the gravitational potential energy 'E_g' of each 'cN' will be (factoring out the weight and acceleration of 'g'): 1kg * g * (5.5 + 4.5 + 3.5 + 2.5 + 1.5 + 0.5) = 18 Joules
5. Moving 3 containers to the other side, leaves container 'X' with: 1kg * g * (2.5 + 1.5 + 0.5) = 4.5 Joules
6. 4.5 / 18 = 1/4 starting amount
7. Container 'Y' now has same amount (4.5 Joules)
8. 4.5 + 4.5 = 9 Joules
9. 9 Joules is half of the starting 18 Joules

Can you not use the center of mass for each cN to calculate its E_g?

 

[Doc Al]

Your analysis looks fine to me. Why do you think it's wrong?

Initial PE: mg(h/2)
Final PE: mg(h/4)

 

[BvU]

Again: your starting amount is not $mgh$ but $mg{h\over2}$ : the average height counts.
You lose 1/2 of this and are left with $mg{h\over 4}$ -- so you lose $mg{h\over 4}$

 

[lerngen]

, I now see where my blind spots were/are. Due to the wording of the question I was focused on 'mgh' as stand-in for E_g and was zeroed-in on fractional amounts of that. Instead this problem is really a question about center of mass and how that affects calculations of height for an object. Further, up to now I realize my unexamined assumption of 'h' in physics problem was the height from the ground to the bottom of an object (hence my attempt to create containers; my initial approach didn't use 0.5 center of mass).

Now that I think about it I've never seen an explanation of center of mass as relates to calculation of height of an object in any introductory physics textbooks I've used. Am I just missing the section in physics books where this is talked about? Or is this supposed to be just generally obvious? Thanks for your patience

 

[BvU]

Actually (and ironically) your own energy calculation is making use of this 'average height' !

Basically what you are doing is going to be correct only if you use infinitely thin sheets of water at height $x$ with a thickness of $dx$ and a mass of $\rho A\; dx$ where $A$ is the area of a container.
Such a sheet has potential energy $\rho g A x \; dx$ and for the whole content you get $$E = \int_0^h \rho g A \; dx = \rho A \int_0^h xdx = \rho A {1 \over 2} h^2 $$ With $M = \rho A h$ this gives $E = {1\over 2 } M h$

And you have just derived the equation for the height of the center of mass.
In most exercises you work with point masses, but not here.

 

[lerngen]

Ah! That ties everything together in a very direct, concrete way. I did briefly think of applying calculus but thought it would result in a mass-less container of water (and what other effects that might have on other physics assumptions) as the container height went to zero. Should have stuck with that train of thought after all.

Thanks again for your time and help.