Troubleshooting N-Spherical Cap Area Formula

[olgerm]

I am trying to understand N-spherical cap area formula (surface area of blue part), but it seems to give wrong answers.

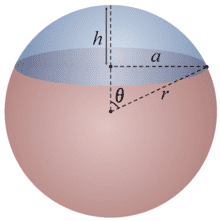
for 1 dimensional cap obviously $\frac{l_{cap}}{l_{sphere}}=\frac{l_{arc}}{l_{circle}}=\frac{r*θ}{r*2π}=\frac{θ}{2π}$

But according to wikipedia formula $\frac{l_{cap}}{l_{sphere}}=\frac{I(\frac{(2r-h)h}{r^2},\frac{n}{2},\frac{1}{2})}{2}$
https://en.wikipedia.org/wiki/Spherical_cap#Hyperspherical_cap

since $h=r(1-cos(θ))$
$I(a,b,c)=\int_0^a (dx*x^{b-1}*(1-x)^{c-1})$ (incomplete beta function)
and $n=1$

$\frac{l_{cap}}{l_{sphere}}=\int_0^{sin^2(θ)} (\frac{dx}{\sqrt{x-x^2}})/2$

But
$\int_0^{sin^2(θ)} (\frac{dx}{\sqrt{x-x^2}})≠\frac{θ}{2π}$
Where is mistake?

 

[Svein]

for 1 dimensional cap obviously lcaplsphere=larclcircle=r∗θr∗2π=θ2πlcaplsphere=larclcircle=r∗θr∗2π=θ2π \frac{l_{cap}}{l_{sphere}}=\frac{l_{arc}}{l_{circle}}=\frac{r*θ}{r*2π}=\frac{θ}{2π}

Look at your figure. You have an angle θ on both sides of h. Therefore, the ratio is θ/π. Sanity check: If θ=π/2, the blue part is half the circle - which agrees with my revised expression.

 

[olgerm]

Look at your figure. You have an angle θ on both sides of h. Therefore, the ratio is θ/π. Sanity check: If θ=π/2, the blue part is half the circle - which agrees with my revised expression.

You are right ,but still
$\int_0^{sin^2(θ)} (\frac{dx}{\sqrt{x-x^2}})/2≠\frac{θ}{π}$

 

[olgerm]

So can anybody derive 1- or 2-dimensional spherical cap formula from N-spherical cap formula?