i-am
- 3
- 0
Hello!
I'm new here, and already did a search. Sorry if the answer is elsewhere, I just couldn't find it!
I'm writing a sci-fi novel and have been brushing up on general and special relativity.
I'm running into a small problem with the twin paradox, and how to describe it from another planets point of view. Maybe I'm not understanding it because I have the math wrong, so please bear with me.
Disregard speeding up and slowing down, Earth math goes:
if
t=2d/v
then if the travel distance between two planets is 6 light years and we are traveling at .8c, then
t=2(6)/.8c= then t=15
So 15 years of travel time @ 80% the speed of light from Earth to Planet A.
if the Lorentz factor holds
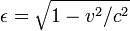 then E=.6 as the time aged on ships clocks and and travelers age.
then E=.6 as the time aged on ships clocks and and travelers age.
So the pilot of the ship would have aged 6 years, but on Earth people would have aged 15 years by the time the traveler would have reached planet A.
I'm sorry if this is incorrect. I haven't taken a physics class in a long time and I'm getting a lot of this math from wiki, and other various websites.
But if I am on Planet B, and I have 30 hours in a day, and 487 days in a year, then will all the math above still hold?
If light travels at 186282 miles per second no matter what planet one is on, and I am on Planet B trying to make sense of the twin paradox for the first time, will my traveling twin still have only aged 6 years, and I 15, planet B time?
For some reason this doesn't make sense in my head.
So I'm wondering if I'm missing something else here.
I'm new here, and already did a search. Sorry if the answer is elsewhere, I just couldn't find it!
I'm writing a sci-fi novel and have been brushing up on general and special relativity.
I'm running into a small problem with the twin paradox, and how to describe it from another planets point of view. Maybe I'm not understanding it because I have the math wrong, so please bear with me.
Disregard speeding up and slowing down, Earth math goes:
if
t=2d/v
then if the travel distance between two planets is 6 light years and we are traveling at .8c, then
t=2(6)/.8c= then t=15
So 15 years of travel time @ 80% the speed of light from Earth to Planet A.
if the Lorentz factor holds
So the pilot of the ship would have aged 6 years, but on Earth people would have aged 15 years by the time the traveler would have reached planet A.
I'm sorry if this is incorrect. I haven't taken a physics class in a long time and I'm getting a lot of this math from wiki, and other various websites.
But if I am on Planet B, and I have 30 hours in a day, and 487 days in a year, then will all the math above still hold?
If light travels at 186282 miles per second no matter what planet one is on, and I am on Planet B trying to make sense of the twin paradox for the first time, will my traveling twin still have only aged 6 years, and I 15, planet B time?
For some reason this doesn't make sense in my head.
So I'm wondering if I'm missing something else here.
Last edited: