mfratczak88
- 8
- 0
- Homework Statement
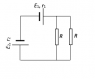
- In the figure below, two batteries with emf E1 and E2 and internal resistances r1 and r2 forms a circuit together with two identical resistors each with resistance R. Find the current passing through each resistor.
- Relevant Equations
- KVL
It's ABCD question with answers attached.
Problem is that, I don't think that neither of those are correct. From KVL the equation seems to be i = (E2-E1)/(2r1+2r2 + R). I've attached images of the circuit, answers, and my solution.
Can someone please point me if I am wrong, and if yes, where's the error ?
Many thanks :)
Edit: It seems that for some reason Images of the solutions cannot be uploaded. None the less here's my solution:
Initial current i1 will produce two currents i2 and i3 so that from KCL we have i1 = i2+i3.
From KVL
1) -E1 + E2 - i1r1 -i1r2 - i2R = 0
2) -i3R+i2R = 0 => i2 = i3
using the fact that i2=i3 and i1 = i2+i3 we have
-E1+E2 - 2*(i2r1) - 2*(i2r2) - i2R = 0 => i2 = (E2-E1)/(2r1+2r2+R).
Problem is that, I don't think that neither of those are correct. From KVL the equation seems to be i = (E2-E1)/(2r1+2r2 + R). I've attached images of the circuit, answers, and my solution.
Can someone please point me if I am wrong, and if yes, where's the error ?
Many thanks :)
Edit: It seems that for some reason Images of the solutions cannot be uploaded. None the less here's my solution:
Initial current i1 will produce two currents i2 and i3 so that from KCL we have i1 = i2+i3.
From KVL
1) -E1 + E2 - i1r1 -i1r2 - i2R = 0
2) -i3R+i2R = 0 => i2 = i3
using the fact that i2=i3 and i1 = i2+i3 we have
-E1+E2 - 2*(i2r1) - 2*(i2r2) - i2R = 0 => i2 = (E2-E1)/(2r1+2r2+R).
Attachments
Last edited: