- #1
Winzer
- 598
- 0
Homework Statement
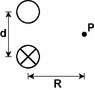
Two long parallel wires are a center-to-center distance of 1.50 cm apart and carry equal anti-parallel currents of 1.80 A. Find the magnetic field intensity at the point P which is equidistant from the wires. (R = 4.00 cm).
Homework Equations
[tex] B= \frac{u_{0}I}{2\pi r} [/tex] infinite wire
The Attempt at a Solution
Ok I have been workin this problem for a while.
In terms of vectors, the y's cancel out.
For the X direction I get:
[tex] B_{totalx}=\frac{u_{0} I R}{\pi \sqrt( (d/2)^2 +R^2)}[/tex]
I don't get why I am wrong, I took the sum of the b-fields in terms of vectors.
And no the answer is not 0 T!