Two particle interference (entanglement)

Thread starter 4everlonging
Start date Oct 30, 2011
Tags

Entanglement Interference Particle

AI Thread Summary

The discussion centers on a scenario involving pairs of particles emitted in opposite directions, with a 50% probability for each direction. When these particles are combined at a 50/50 beam splitter, the interference pattern becomes a key focus. Participants analyze how the indistinguishability of the particle paths affects detection rates at the detectors. The outcome reveals that due to quantum interference, the detection percentages at each detector will not simply reflect the initial emission probabilities. Overall, the analysis emphasizes the complex nature of quantum entanglement and interference in particle detection.

Oct 30, 2011

4everlonging

Homework Statement

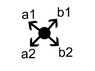
A source emits pairs of particles "back to back", 50% into directions a1 and b1, 50 % into directions a2 and b2, where the choice between a1+b1 and a2+b2 is fundamentally undetermined.

Insert Diagram A

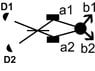
suppose that directions a1 and a2 are combined on a 50/50 beam splitter(equal path lengths)

Insert Diagram B

what percentage of the particles emitted to the left will be detected in each detector?

Physics news on Phys.org

Oct 31, 2011

4everlonging

what?

Thread 'I've come across another fluid pressure problem I don't understand'

Neglect gravity other than that of water; neglect friction. F1=ρgsh=1000*10*1*(1+4)=50000 N; F1=ρgsh=1000*10*0.1*4=4000 N; F3=50000-4000=46000 N?

View full post »

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...

View full post »

Thread 'Struggle to understand the concept of the question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...

View full post »