Two-port linear network general representation AV + BI = 0

[cianfa72]

TL;DR Summary

Two-port linear network general representation AV + BI = 0. It seems that it might exist a two-port linear network having a representation of 3 linear homogeneous independent equations

Hi,
as follow-up to this thread I've a question about general representation of a two-port network.

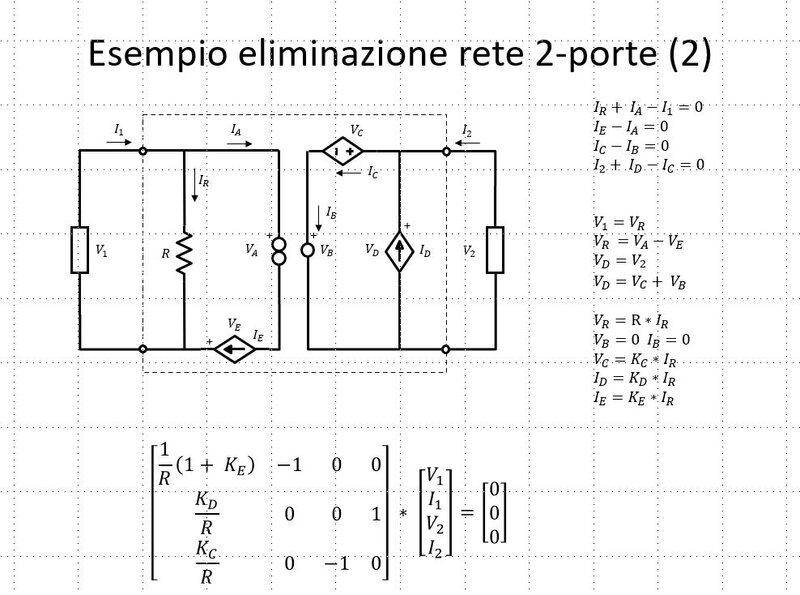Basically it is ad hoc built four-terminal linear network (using controlled sources + nullator-norator pair): for it I found a general representation $AV + BI = 0$ as in the picture above.

If I did the job correctly, Gauss elimination of internal variables (voltages & currents of internal elements) results in 3 linear homogeneous independent equations in port variables V1,I1,V2,I2.

Now, on various circuit theory sources, I found that any two-port linear network (with no internal independent sources) can always be represented in the general form $AV + BI = 0$ where $A$ e $B$ are two 2x2 matrices (the two equations, actually, could be dependent each other).

Thus, from this example, it seems that it might exist a two-port representation having 3 linear homogeneous independent equations !

What do you think about ? Thanks.

 

[eq1]

There are 4 variables for three equations so there has to be either no solution or infinitely many. Assuming the matrix is setup correctly (didn't double check it), it can't be inconsistent (because the circuit exists), so it must have infinitely many. If that's true then they're not independent equations.

 

[cianfa72]

There are 4 variables for three equations so there has to be either no solution or infinitely many. Assuming the matrix is setup correctly (didn't double check it), it can't be inconsistent (because the circuit exists), so it must have infinitely many. If that's true then they're not independent equations.

Thanks for the reply. Yes, there are 3 independent equations in 4 port variables coming from Gauss elimination of the quadripole internal element's variables.

The point then is that those 3 equations are part of a system of equations for the entire electrical network the quadripole is part of. So the overall network might be also inconsistent though.

 

[Jody]

I haven’t seen the equation $AV+BI=0$. What is it? I feel very uneasy about adding voltages and currents together, but I have seen similar with ABCD and h-parameters…. it doesn’t look to me, that you are trying ABCD nor h-parameters especially with the output being zero? When I look at your system of equations based on the matrix the first two equations look like you're adding currents possibly KCL because the voltage is multiplied by what looks like conductance, but that third equation it looks to me you're adding voltage and current together, which looks odd to me. Your derivation was hard for me to follow because so many different notations and letters like i have no idea where $K$ came from.

If $AV+BI=0$ is really something is there any chance you can point to me where you've seen that before or maybe provide to me a very simple example using it on a class voltage divider or pi-network? My first thoughts on it is... it's a very unintuitive way of using Ohm's law where $R$ is $-B/A$?? Forgive me if I'm being silly or if it should be obvious... this is not an approach I'm familiar with, but would be happy to learn.

 

[DaveE]

Sorry, I kind of gave up with your network schematic. You have, I think, 4 different symbols for voltage sources. You have, I think, a current source drawn in series with a voltage source. You have branches with current sources set to zero. You have the same quantities defined twice, with two variables. This is all too confusing for me to want to sort out. My initial reaction would be to simplify first and eliminate all of the extraneous stuff. You will generate more reader interest that way, especially among those of us that don't want to play a "find Waldo" sort of game.

Also your network theorem AV + BI = 0 doesn't mean much to me since I don't know what V and I are. I suppose any linear circuit could be defined that way, depending on how you define A, B, V, and I.

 

[cianfa72]

Sorry, I kind of gave up with your network schematic. You have, I think, 4 different symbols for voltage sources. You have, I think, a current source drawn in series with a voltage source. You have branches with current sources set to zero. You have the same quantities defined twice, with two variables. This is all too confusing for me to want to sort out. My initial reaction would be to simplify first and eliminate all of the extraneous stuff.

Why ? I employed just a symbol for the current-controlled voltage source V_C and another one for the two current-controlled current source I_D and I_E. The two 'external' bipoles are just two bipoles with no BCE (Branch Constitutive Equation ) for each of them. Basically they are actually indeterminate.

Also your network theorem AV + BI = 0 doesn't mean much to me since I don't know what V and I are. I suppose any linear circuit could be defined that way, depending on how you define A, B, V, and I.

$\mathrm {V}$ and $\mathrm {I}$ are actually two vectors: $\mathrm {V}$ is the vector of port voltages V₁, V₂ and $\mathrm {I}$ is the vector of port currents I₁, I₂.

 

[cianfa72]

I haven’t seen the equation $AV+BI=0$. What is it? I feel very uneasy about adding voltages and currents together, but I have seen similar with ABCD and h-parameters…. it doesn’t look to me, that you are trying ABCD nor h-parameters especially with the output being zero?

Sorry, I've just a reference to it in my Italian circuit theory book. It is not ABCD or h-parameters.
It is just a general network representation that always exist for any two-port linear network (quadripole). Starting from it you can 'derive' a specific representation (if it actually does exist) such as h-parameters, z-parameter, y-parameter and so on...

 

[DaveE]

I'm not sure what your doing with this network. But, I don't see why you set I_B = 0. Then you don't follow through with all of the simplifications that result. I guess you like canonical forms and matrices with lots of zeros. That's great if you are programming a generic circuit simulator, but this is really simple to do with KVL, etc. BTW, with I_B = 0, V₂ is determined solely by the load impedance.

A couple of things to consider:
1) Any voltage source in series with a current source can be deleted with no change to the solution (it only effects the voltage across the current source).
2) Any current source in parallel with a voltage source can be deleted with no change to the solution (it only effects the current through the voltage source).
3) Any branch with zero current can be deleted (replaced with an open circuit).
4) Any branch with zero voltage can be replaced with a short circuit.

Edit: On 2nd thought, I_B = 0 must be a typo. You probably didn't mean it, it makes the problem too simple. Although I still don't understand what the problem your addressing is, that's my fault for not paying enough attention, I think.

 

[cianfa72]

I'm not sure what your doing with this network. But, I don't see why you set IB = 0. Then you don't follow through with all of the simplifications that result. I guess you like canonical forms and matrices with lots of zeros.

Sorry, maybe it wasn't clear from the schematic: the circle with the symbol V_B is a nullator, the other one on the left (double circle) is instead a norator; that pair forms a Nullor

 

[cianfa72]

Sorry, I've just a reference to it in my Italian circuit theory book. It is not ABCD or h-parameters.
It is just a general network representation that always exist for any two-port linear network (quadripole). Starting from it you can 'derive' a specific representation (if it actually does exist) such as h-parameters, z-parameter, y-parameter and so on...

I found a reference to it in the book: Linear and non linear circuits - L. Chua, C. Desoer, E. Kuh - chapter 13, section 2.

 

[DaveE]

Sorry, maybe it wasn't clear from the schematic: the circle with the symbol V_B is a nullator, the other one on the left (double circle) is instead a norator; that pair forms a Nullor

OK, I think I understand your notation now (although I'm still not crazy about the representation of voltage sources in series with current sources). I was working under the impression that this was a model for a physically realizable system, but the constraints on both I₂ and V₂ make it singular.

Let's look at an example case:
Set V₁ = 1V, R = K_C = 1Ω, K_E = K_D = 1
Then I₂ = -1A and V₂ = 1V independent of whatever is connected to the right side port. What happens if I connect a 2Ω resistor there?

What's the point?

 

[cianfa72]

I was working under the impression that this was a model for a physically realizable system, but the constraints on both I₂ and V₂ make it singular.

No, it is not. It is just an 'ad hoc' network conceived by me.

Let's look at an example case:
Set V1 = 1V, R = KC = 1Ω, KE = KD = 1
Then I2 = -1A and V2 = 1V independent of whatever is connected to the right side port. What happens if I connect a 2Ω resistor there?

What's the point?

ok, thus the port on the left is attached to a 1V independent voltage source.
In this case the complete network the quadripole (two-port network) is member of, has actually not solution ! In other words basically that network is 'impossible' !